Advertisements
Advertisements
Question
आकृतीमध्ये, ΔABC हा समभुज त्रिकोण आहे. ∠B चा कोनदुभाजक ΔABC च्या परिवर्तुळाला बिंदू P मध्ये छेदत असेल, तर सिद्ध करा: CQ = CA.
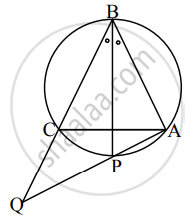
Solution
ΔABC हा समभुज त्रिकोण आहे.
∴ ∠ABC = ∠ACB = ∠BAC = 60° .....(i) [समभुज त्रिकोणाचे कोन]
∠CBP = `1/2`∠ABC ........[किरण BP ∠B ला दुभागतो.]
∴ ∠CBP = `1/2 xx 60^circ` ....[(i) वरून]
∴ ∠CBP = 30°
∠CBP = ∠CAP = 30° ..........…[एकाच कंसात अंतर्लिखित केलेले कोन]
∴ ∠CAQ = 30° …(ii) [A - P - Q]
ΔABC मध्ये,
∠BAQ = ∠BAC + ∠CAQ ........[कोनांच्या बेरजेचा गुणधर्म]
∴ ∠BAQ = 60° + 30° .......[(i) व (ii) वरून]
∴ ∠BAQ = 90°
तसेच, ∠ABQ = 60° .......[(i) व B - C - Q वरून]
∴ ∠BQA = 30° ...[ΔABQ चा उर्वरित कोन]
∴ ∠CQA = 30° .....(iii) [B - C - Q]
ΔCQA मध्ये,
∠CAQ = ∠CQA ......[(ii) व (iii) वरून]
∴ CQ = CA ...........[समद्विभुज त्रिकोणाच्या प्रमेयाचा व्यत्यास]
APPEARS IN
RELATED QUESTIONS
रेख XZ व्यास असलेल्या वर्तुळाच्या अंतर्भागात Y हा एक बिंदू आहे. तर खालीलपैकी किती विधाने सत्य आहेत?
(i) ∠XYZ हा लघुकोन असणे शक्य नाही.
(ii) ∠XYZ हा काटकोन असणे शक्य नाही.
(iii) ∠XYZ हा विशालकोन आहे.
(iv) ∠XYZ च्या मापासंबंधी निश्चित विधान करता येणार नाही.
प्रत्येक उपप्रश्नासाठी चार पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक पर्याय निवडा.
अर्धवर्तुळात अंतर्लिखित केलेल्या कोनाचे माप किती असते?
खालील आकृतीमध्ये, ∠PQR = 50°, तर ∠PSR चे माप काढा?

आकृतीमध्ये, ∠ABC = 35°, तर m(कंस AXC) काढा?
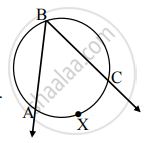
अर्धवर्तुळात अंतर्लिखित झालेला कोन काटकोन असतो हे पुढील कृतीद्वारे सिद्ध करा.

पक्ष : केंद्र M असलेल्या अर्धवर्तुळात ∠ABC अंतर्लिखित कोन आहे.
साध्य : ∠ABC हा काटकोन आहे.
सिद्धता: अंतर्लिखित ∠ABC ने कंस AXC अंतर्खंडित केला आहे.
रेख AC हा वर्तुळाचा व्यास आहे.
m(कंस AXC) = `square`
तसेच, ∠ABC = `square` ...........…[अंतर्लिखित कोनाचे प्रमेय]
= `1/2 xx square`
∴ ∠ABC = `square`
∴ ∠ABC हा काटकोन आहे.
वर्तुळाच्या जीवा AB आणि CD परस्परांना त्याच वर्तुळाच्या अंतर्भागातील बिंदू M मध्ये छेदतात, तर CM × BD = BM × AC हे सिद्ध करा.
