Advertisements
Advertisements
Question
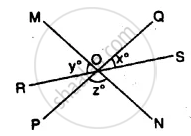
AB, CD and EF are three lines intersecting at the same point.
(i) Find x, if y = 45° and z = 90°.
(ii) Find a, if x = 3a, y = 5x and r = 6x.
Solution
AB, CD and EF are intersecting each other at O.
and ∠DOF = x°, ∠AOC = y°
and ∠BOE = z°
But ∠DOB = ∠AOC = y° ...............(Vertically opposite angles)
Similarly, ∠COE = ∠DOF = x°
and ∠AOF = ∠BOE = z°
∴ CD is a straight line
∴ ∠COE + ∠BOE + ∠DOE = 180°
⇒ x° + z° + y° = 180°
⇒ x° + y° + z° = 180°
(i) If y = 45°, and z = 90°, then
⇒ x° + 45° + 90° = 180°
⇒ x° + 135° = 180°
∴ x° = 180°− 135° = 45°
(ii) If x = 3a, y = 5x, z = 6x,
then x + y + z = 180°
⇒ x + 5x + 6x = 180°
⇒ 12x = 180°
⇒ x = `(180°)/12` = 15°
But x = 3a
∴ 3a = 15°
⇒ a = `(15°)/3` = 5°
Hence a = 5°
APPEARS IN
RELATED QUESTIONS
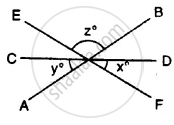
In below fig, determine the value of x.

Fill in the blank so as to make the following statement true:
If the sum of two adjacent angles is 180°, then the ______ arms of the two angles are
opposite rays
If two straight lines intersect each other, prove that the ray opposite to the bisector of one of the angles thus formed bisects the vertically opposite angle.
Define complementary angles.
The supplement of an acute angle is .................
Write the supplement of an angle of measure 2y°.
In the following figure, ∠AOB and ∠AOC are adjacent angles? Give the reason for your answer.
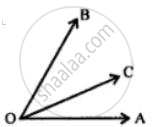
In the given figure, find ∠PQR.
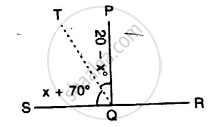
Write the complement of 21° 17'
In the given figure, lines PQ, MN, and RS intersect at O. If x : y = 1 : 2 and z = 90°, find ∠ROM and ∠POR.