Question

AB is a chord of a circle centred at O such that ∠AOB = 60°. If OA = 14 cm, then find the area of the minor segment. `("take" sqrt3 = 1.73)`

Answer 1

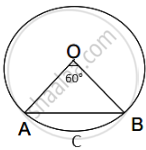
Let ACB be given the subtending angle of 60° at the centre.

∵ θ = 60° and OA = OB

∴ ΔOAB is an equilateral triangle.

Here, r = 14 cm and θ = 60°

Area of minor Segment = Area of sector OACBO − Area of ΔOAB

= `θ/(360°) xx πr^2 − sqrt3/4r^2`

= `(60°)/(360°) xx 22/7 xx (14  cm)^2 − sqrt3/4 xx (14  cm)^2`

= `60/360 xx 22/7 xx 14  cm xx 14  cm − sqrt 3/4 xx 14  cm xx 14  cm`

= `(22 xx 14)/3  cm^2 − 49 sqrt3  cm^2`

= `308/3  cm^2 − 49 xx 1.732  cm^2`

= 102.67 cm² − 84.87 cm²

= 17.8 cm²