English Medium
Academic Year: 2024-2025
Date: March 2025
Advertisements
General Instructions:
Read the following instructions carefully and follow them:
- This question paper contains 38 questions.
- This Question Paper is divided into 5 Sections A, B, C, D and E.
- In Section A, Questions no. 1-18 are multiple choice questions (MCQs) and questions no. 19 and 20 are Assertion- Reason based questions of 1 mark each.
- In Section B, Questions no. 21-25 are very short answer (VSA) type questions, carrying 02 marks each.
- In Section C, Questions no. 26-31 are short answer (SA) type questions, carrying 03 marks each.
- In Section D, Questions no. 32-35 are long answer (LA) type questions, carrying 05 marks each.
- In Section E, Questions no. 36-38 are case study based questions carrying 4 marks each with sub parts of the values of 1, 1 and 2 marks each respectively.
- All Questions are compulsory. However, an internal choice in 2 Question of Section B, 2 Questions of Section C and 2 Questions of Section D has been provided. An internal choice has been provided in all the 2 marks questions of Section E.
- Draw neat and clean figures wherever required.
- Take `pi =22/7` wherever required if not stated.
- Use of calculators is not allowed.
The graph of a quadratic polynomial p(x) passes through the points (−6, 0), (0, −30), (4, −20) and (6, 0). The zeroes of the polynomial are __________.
−6, 0
4, 6
−30, −20
−6, 6
Chapter:
The value of k for which the system of equations 3x − ky = 7 and 6x + 10y = 3 is inconsistent, is ______.
−10
−5
5
7
Chapter:
Which of the following statements is not true?
A number of secants can be drawn at any point on the circle.
Only one tangent can be drawn at any point on a circle.
A chord is a line segment joining two points on the circle.
From a point inside a circle only two tangents can be drawn.
Chapter:
If the nth term of an A.P. is 7n − 4, then the common difference of the A.P. is ______.
7
7n
−4
4
Chapter:
The radius of the base of a right circular cone and the radius of a sphere are each 5 cm in length. If the volume of the cone is equal to the volume of the sphere then the height of the cone is ________.
5 cm
20 cm
10 cm
4 cm
Chapter:
If tanθ = `5/2` then `(4 sinθ + cosθ)/(4sinθ − cosθ)` is equal to ________.
`11/9`
`3/2`
`9/11`
4
Chapter:
In the given figure, a tangent has been drawn at a point P on the circle centred at O.
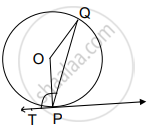
If ∠TPQ = 110°, then ∠POQ is equal to:
110°
70°
140°
55°
Chapter:
A quadratic polynomial having zeroes `-sqrt(5/2)` and `sqrt(5/2)` is _________.
`x^2 − 5sqrt2 x + 1`
8x2 − 20
15x2 − 6
`x^2 - 2sqrt5 x - 1`
Chapter:
Consider the frequency distribution of 45 observations.
| Class | 0 - 10 | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 |
| Frequency | 5 | 9 | 15 | 10 | 6 |
The upper limit of the median class is:
20
10
30
40
Chapter:
O is the point of intersection of two chords AB and CD of a circle.
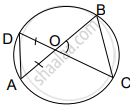
If ∠BOC = 80° and OA = OD then ΔODA and ΔOBC are ____________.
equilateral and similar
isosceles and similar
isosceles but not similar
not similar
Chapter:
The roots of the quadratic equation x2 + x − 1 = 0 are __________.
Irrational and distinct
not real
rational and distinct
real and equal
Chapter:
If θ = 30° then the value of 3tanθ is ________.
1
`1/sqrt3`
`3/sqrt3`
not defined
Chapter:
The volume of a solid hemisphere is `396/7` cm3. The total surface area of the solid hemisphere (in sq. cm) is ______.
`396/7`
`594/7`
`549/7`
`604/7`
Chapter:
In a bag containing 24 balls, 4 are blue, 11 are green and the rest are white. One ball is drawn at random. The probability that drawn ball is white in colour is ________.
`1/6`
`3/8`
`11/24`
`5/8`
Chapter:
The point on the x-axis nearest to the point (-4, -5) is __________.
(0, 0)
(−4, 0)
(−5, 0)
`(sqrt41, 0)`
Chapter:
Which of the following gives the middle most observation of the data?
Median
Mean
Range
Mode
Chapter:
Advertisements
A point on the x-axis divides the line segment joining the points A(2, −3) and B(5, 6) in the ratio 1 : 2. The point is __________.
(4, 0)
`(7/2, 3/2)`
(3, 0)
(0, 3)
Chapter:
A card is drawn from a well shuffled deck of playing cards. The probability of getting red face card is _________.
`3/13`
`1/2`
`3/52`
`3/26`
Chapter:
Assertion (A): HCF of any two consecutive even natural numbers is always 2.
Reason (R): Even natural numbers are divisible by 2.
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
Both assertion (A) and reason (R) are true and reason (R) is not the correct explanation of assertion (A).
Assertion (A) is true but reason (R) is false.
Assertion (A) is false but reason (R) is true.
Chapter:
Assertion (A): If the radius of sector of a circle is reduced to its half and angle is doubled then the perimeter of the sector remains the same.
Reason (R): The length of the arc subtending angle θ at the centre of a circle of radius r = `(pirθ)/180`.
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
Both assertion (A) and reason (R) are true and reason (R) is not the correct explanation of assertion (A).
Assertion (A) is true but reason (R) is false.
Assertion (A) is false but reason (R) is true.
Chapter:
Find the H.C.F and L.C.M of 480 and 720 using the prime factorisation method.
Chapter:
The H.C.F of 85 and 238 is expressible in the form 85m -238. Find the value of m.
Chapter:
Two dice are rolled together bearing numbers 4, 6, 7, 9, 11, 12. Find the probability that the product of numbers obtained is an odd number.
Chapter:
How many positive three-digit integers have the hundredths digit 8 and unit’s digit 5? Find the probability of selecting one such number out of all three-digit numbers.
Chapter:
Evaluate: `(2sin^2 60° − tan^2 30°)/(sec^2 45°)`
Chapter:
Find the point(s) on the x-axis which is at a distance of `sqrt41` units from the point (8, −5).
Chapter:
Show that the points A(−5, 6), B(3, 0) and C(9, 8) are the vertices of an isosceles triangle.
Chapter:
In ΔABC, D, E and F are midpoints of BC, CA and AB respectively. Prove that ΔFBD ∼ ΔDEF and ΔDEF ∼ ΔABC.
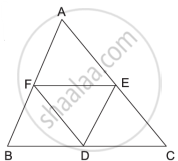
Chapter:
In ΔABC, P and Q are points on AB and AC, respectively, such that PQ is parallel to BC. Prove that the median AD drawn from A on BC bisects PQ.
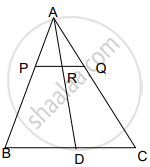
Chapter:
Advertisements
The sum of two numbers is 18 and the sum of their reciprocals is `9/40`. Find the numbers.
Chapter:
If α and β are zeroes of a polynomial 6x2 − 5x + 1 then form a quadratic polynomial whose zeroes are α2 and β2.
Chapter:
If cosθ + sinθ = 1, then prove that cosθ − sinθ = ±1.
Chapter:
The minute hand of a wall clock is 18 cm long. Find the area of the face of the clock described by the minute hand in 35 minutes.
Chapter:
AB is a chord of a circle centred at O such that ∠AOB = 60°. If OA = 14 cm, then find the area of the minor segment. `("take" sqrt3 = 1.73)`
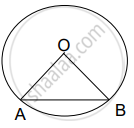
Chapter:
Prove that `sqrt3` is an irrational number.
Chapter: [0.011000000000000001] Real Numbers
Solve the following system of linear equations graphically:
x + 2y = 3, 2x − 3y + 8 = 0
Chapter:
Places A and B are 180 km apart on a highway. One car starts from A and another from B at the same time. If the car travels in the same direction at different speeds, they meet in 9 hours. If they travel towards each other with the same speeds as before, they meet in an hour. What are the speeds of the two cars?
Chapter:
Prove that the lengths of tangents drawn from an external point to a circle are equal.
Using the above result, find the length BC of ΔABC. Given that, a circle is inscribed in ΔABC touching the sides AB, BC and CA at R, P and Q respectively and AB = 10 cm, AQ = 7 cm, CQ = 5 cm.
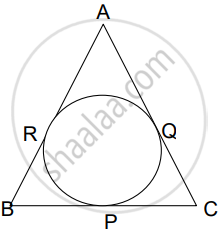
Chapter:
A boy whose eye level is 1.35 m from the ground, spots a balloon moving with the wind in a horizontal line at some height from the ground. The angle of elevation of the balloon from the eyes of the boy at an instant is 60°. After 12 seconds, the angle of elevation reduces to 30°. If the speed of the wind is 3m/s then find the height of the balloon from the ground. `("Use" sqrt3= 1.73)`
Chapter:
Find the mean and median of the following data:
| Class | 85 - 90 | 90 - 95 | 95 - 100 | 100 - 105 | 105 - 110 | 110 - 115 |
| frequency | 15 | 22 | 20 | 18 | 20 | 25 |
Chapter:
The monthly expenditure on milk in 200 families of a Housing Society is given below:
| Monthly Expenditure (in ₹) |
1000 – 1500 | 1500 – 2000 | 2000 – 2500 | 2500 – 3000 | 3000 – 3500 | 3500 – 4000 | 4000 – 4500 | 4500 – 5000 |
| Number of families | 24 | 40 | 33 | x | 30 | 22 | 16 | 7 |
Find the value of x and also, find the median and mean expenditure on milk.
Chapter: [0.071] Statistics
|
Ms. Sheela visited a store near her house and found that the glass jars are arranged one above the other in a specific pattern. On the top layer, there are 3 jars. In the next layer, there are 6 jars. In the 3rd layer from the top there are 9 jars and so on till the 8th layer. |
On the basis of the above situation, answer the following questions:
- Write an A.P. whose terms represent the number of jars in different layers starting from top. Also, find the common difference.
- Is it possible to arrange 34 jars in a layer if this pattern is continued? Justify your answer.
-
- If there are ‘n’ number of rows in a layer, then find the expression for finding the total number of jars in terms of n. Hence, find S8.
OR - The shopkeeper added 3 jars in each layer. How many jars are there in the 5th layer from the top?
- If there are ‘n’ number of rows in a layer, then find the expression for finding the total number of jars in terms of n. Hence, find S8.
Chapter:

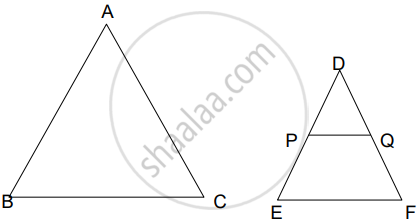
Triangle is a very popular shape used in interior designing. The picture given above shows a cabinet designed by a famous interior designer.
Here the largest triangle is represented by ΔABC and smallest one with shelf is represented by ΔDEF. PQ is parallel to EF.
- Show that ΔDPQ ∼ ΔDEF.
- If DP = 50 cm and PE = 70 cm then find `(PQ)/(EF)`.
-
- If 2AB = 5DE and ΔABC ∼ ΔDEF then show that `"perimeter of ΔABC"/"perimeter of ΔDEF"` is constant.
OR - If AM and DN are medians of triangles ABC and DEF respectively then prove that ΔABM ∼ ΔDEN.
- If 2AB = 5DE and ΔABC ∼ ΔDEF then show that `"perimeter of ΔABC"/"perimeter of ΔDEF"` is constant.
Chapter:
|
Metallic silos are used by farmers for storing grains. Farmer Girdhar has decided to build a new metallic silo to store his harvested grains. It is in the shape of a cylinder mounted by a cone. Dimensions of the conical part of a silo are as follows: Dimensions of the cylindrical part of a silo are as follows: |
On the basis of the above information, answer the following questions:.
- Calculate the slant height of the conical part of one silo.
- Find the curved surface area of the conical part of one silo.
-
- Find the cost of metal sheet used to make the curved cylindrical part of 1 silo at the rate of ₹ 2000 per m2.
OR - Find the total capacity of one silo to store grains.
- Find the cost of metal sheet used to make the curved cylindrical part of 1 silo at the rate of ₹ 2000 per m2.
Chapter:
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CBSE previous year question papers Class 10 Mathematics with solutions 2024 - 2025
Previous year Question paper for CBSE Class 10 Maths-2025 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CBSE Class 10.
How CBSE Class 10 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
