Question

Metallic silos are used by farmers for storing grains. Farmer Girdhar has decided to build a new metallic silo to store his harvested grains. It is in the shape of a cylinder mounted by a cone. Dimensions of the conical part of a silo are as follows: Radius of base = 1.5 m Height = 2 m Dimensions of the cylindrical part of a silo are as follows: Radius = 1.5 m Height = 7 m

On the basis of the above information, answer the following questions:.

1. Calculate the slant height of the conical part of one silo.
2. Find the curved surface area of the conical part of one silo.
3. 1. Find the cost of metal sheet used to make the curved cylindrical part of 1 silo at the rate of ₹ 2000 per m².
                                         OR
   2. Find the total capacity of one silo to store grains.

Answer 1

i.

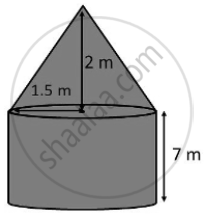
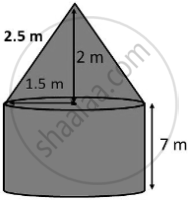
Radius of cone (r) = 1.5 cm

Height of cone (h) = 2m

Slant Height (l) = `sqrt((h)^2 + (r)^2)`

= `sqrt((2)^2 + (1.5)^2`

= `sqrt((2)^2 + (3/2)^2`

= `sqrt(4 + 9/4)`

= `sqrt((16 + 9)/4)`

= `sqrt(25/4)`

= `5/2`

l = 2.5 m

ii.

The curved surface area of the cone

= πrl

= `22/7 xx 1.5 xx 2.5`

= `22/7 xx 3.75`

= `82.5/7`

= 11.78 m²

iii. A. Radius of Cylinder (r) = 1.5m

Height of Cylinder (h) = 7

Curved Surface area of Cylinder = 2πrh

= `2 xx 22/7 xx 1.5 xx 7`

= 2 × 22 × 1.5

= 66 m²

Cost of the metal sheet for 1 m² = Rs. 2000

The cost of the metal sheet for 66 m² = Rs. 2000 × 66

= Rs. 1,32,000

Hence,

Total cost = Rs. 1,32,000

OR

B. Total Capacity = Volume of Cone + Volume of Cylinder

= `1/3πr^2 h + πr^2 h`

= `πr^2 (1/3 h + h)`

= `22/7 xx (1.5)^2 (1/3 xx 2 + 7)`

= `22/7 xx (3/2)^2 (2/3 + 7/1)`

= `22/7 xx 9/4 ((2 + 21)/3 )`

= `99/14 xx 23/3`

= `759/14`

= 54.21 m³