Question

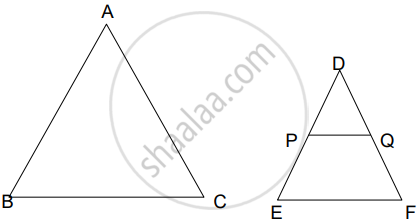
Triangle is a very popular shape used in interior designing. The picture given above shows a cabinet designed by a famous interior designer.

Here the largest triangle is represented by ΔABC and smallest one with shelf is represented by ΔDEF. PQ is parallel to EF.

1. Show that ΔDPQ ∼ ΔDEF.
2. If DP = 50 cm and PE = 70 cm then find `(PQ)/(EF)`.
3. 1. If 2AB = 5DE and ΔABC ∼ ΔDEF then show that `"perimeter of ΔABC"/"perimeter of ΔDEF"` is constant.
                                            OR
   2. If AM and DN are medians of triangles ABC and DEF respectively then prove that ΔABM ∼ ΔDEN.

Answer 1

i. Given, PQ || EF

And, DE as transversal

∴ ∠DPQ = ∠DEF  ...[∵ Correspoing angles]

∠DQP = ∠DFE

In ΔDPQ and ΔDEF

∠DPQ = ∠DEF

∠DQP = ∠DFE

∴ ΔDPQ ∽ ΔDEF  ...[AA Similarity]

Hence Proved.

ii. ΔDPQ ∽ ΔDEF

We know that,

The sides of similar triangles are proportional.

`(DP)/(DE)` = `(PQ)/(EF)`

`(DP)/(DP + PE)` = `(PQ)/(EF)`

`50/(50 + 70)` = `(PQ)/(EF)`

`50/120` = `(PQ)/(EF)`

∴ `(PQ)/(EF)` = `5/12`

iii. A.

Given,

2AB = 5DE

`(AB)/(DE)` = `5/2`

ΔABC ∽ ΔDEF

So, the sides of similar triangles are proportional.

`(AB)/(DE) = (BC)/(EF) = (AC)/(DF)`

Since `(AB)/(DE)` = `5/2`

Therefore,

`(AB)/(DE)` = `(AC)/(DF)` = `(BC)/(EF)` = `5/2`

∴ AB = `5/2 DE`, AC = `5/2DF`, BC = `5/2EF`

Now,

`"Perimeter of ΔABC"/"Perimeter of ΔDEF"` = `(AB + AC + BC)/(DE + DF + EF)`

= `(5/2 DE + 5/2 DF + 5/2 EF)/(DE + DF + EF)`

= `(5/2 DE + DF + EF)/(DE + DF + EF)`

= `5/2`

Thus,

`"Perimeter of ΔABC"/"Perimeter of ΔDEF"` = `5/2` is constant.

OR

B.

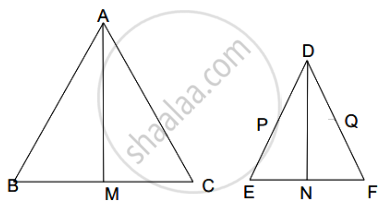
Given,

AM and DN are medians.

Since AM is the median,

M is the mid-point of BC.

∴ BM = CM = `1/2 BC`

Also, DN is median,

N is the mid-point of EF.

∴ EN = FN = `1/2EF`

ΔABC ∽ ΔDEF

The sides of similar triangles are proportional.

So,

`(AB)/(DE)` = `(AC)/(DF)` = `(BC)/(EF)`

`(AB)/(DE)` = `(BC)/(EF)`

`(AB)/(DE)` = `(2BM)/(2EN)`

`(AB)/(DE)` = `(BM)/(EN)`  ...(i)

Also, ∠B = ∠E  ....(ii)

In ΔABM and ΔDEN

∠B = ∠E

`(AB)/(DE)` = `(BM)/(EN)`

∴ ΔABM ∽ ΔDEN  ...[SAS Similarly]

Hence Proved.