Advertisements
Advertisements
Question
In ΔABC, D, E and F are midpoints of BC, CA and AB respectively. Prove that ΔFBD ∼ ΔDEF and ΔDEF ∼ ΔABC.
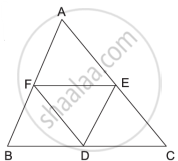
Solution
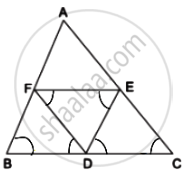
we know that,
The line joining the midpoints of two sides of a triangle is parallel to the 3rd side.
In ΔABC,
F and E are mid-points of AB and AC, respectively,
∴ FE || BC
So, FE || BD ...(1)
Similarly,
D and E are midpoints of BC and AC, respectively.
∴ DE || AB
So, DE || BF ....(2)
from (1) and (2)
FE || BD and DE || BF
Therefore, the opposite sides of the quadrilateral are parallel.
∴ DBEF is a parallelogram.
Similarity,
DCEF is a parallelogram.
Since, DBEF is a parallelogram, and in parallelogram, opposite angles are equal,
∴ ∠DFF = ∠ABC .....(3)
Since DCEF is a parallelogram, and in a parallelogram, opposite angles are equal.
∴ ∠DFF = ∠ACB .....(4)
In ΔDEF and ΔABC
∠DEF and ∠ACB
∠DEF = ∠ABC
∴ ΔDEF ∽ ΔABC ...[AA Similarity Criterion]
In ΔFBD and ΔDEF
∠FBD = ∠DEF
∠BDF = ∠EFD ...[∵ Alternate angles]
∴ ΔFBD ∽ ΔDEF ...[AA Similarity Criterion]
