Question

Prove that the lengths of tangents drawn from an external point to a circle are equal.

Using the above result, find the length BC of ΔABC. Given that, a circle is inscribed in ΔABC touching the sides AB, BC and CA at R, P and Q respectively and AB = 10 cm, AQ = 7 cm, CQ = 5 cm.

Answer 1

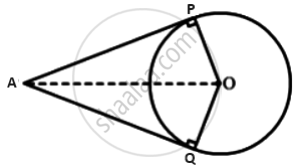
Given:  AP and AQ are two tangents drawn from an external point A.

To Prove: AP = AQ

Construction: Join OP, OQ, and OA

Proof: The tangent at any point of a circle is perpendicular to the radius through the point of contact.

∴ ∠OPA = ∠OQA = 90° ......(i)

In ΔOPA and ΔOQA

OP = OQ  ...(radii of circle)

OA = OA  ...(common)

and ∠OPA = ∠OQA  ....[from equation (i)]

Therefore,

ΔΟΡΑ ≅ ΔΟQA  ...(By RHS)

∴ AP = AQ  ...(Hence proved)

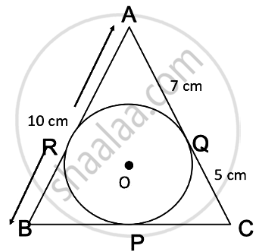
Hence,

AR = AQ = 7 cm

CP = CQ = 5 cm

BP = BR

Since AB = 10 cm and AR = 7 cm

∴ BR = 3 cm

Thus,

BP = BR = 3 cm

Now,

BC = BP + CP

= 3 cm + 5 cm

= 8 cm