Question

A boy whose eye level is 1.35 m from the ground, spots a balloon moving with the wind in a horizontal line at some height from the ground. The angle of elevation of the balloon from the eyes of the boy at an instant is 60°. After 12 seconds, the angle of elevation reduces to 30°. If the speed of the wind is 3m/s then find the height of the balloon from the ground. `("Use"  sqrt3= 1.73)`

Answer 1

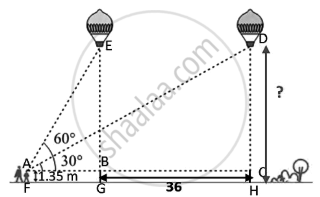
Given that a 1.35 m tall boy sees a balloon.

So, AF = 1.35 m

Also, AF, BG, and CH are parallel.

BG = CH = AF = 1.35 m

Also, given that after 12 seconds, the angle of elevation reduces to 30°. If the speed of the wind is 3 m/s, then find the height of the balloon from the ground.

Therefore,

BC = Distance travelled by balloon due to 3m/s wind in 12 sec

= Speed × Time

= 3 × 12

= 36 m

∴ BC = 36 m

And we need to find the height of the balloon from the ground.

i.e., we need to find DH

Also, the boy sees the balloon first at 60°.

So, ∠EAB = 60°

After travelling, the angle of elevation becomes 30°

So, ∠DAC = 30°

And EG = DH because the height of the balloon from the ground remains the same

Here,

∠ABE = 90° and ∠ACD = 90°

In right angle triangle EBA

tan A = `"Side opposite to angle A"/"Side adjacent to angle A"`

tan A = `(BE)/(AB)`

tan 60° = `(BE)/(AB)`

`sqrt3` = `(BE)/(AB)`

AB = `(BE)/sqrt3`

In an right angle triangle, DAC

tan A = `"Side opposite to angle A"/"Side adjacent to angle A"`

tan A = `(CD)/(AC)`

tan 30° = `(CD)/(AC)`

`1/sqrt3` = `(CD)/(AC)`

AC = `CDsqrt3`

Since BE = CD

∴ AB = `(CD)/sqrt3  "and"  AC = CD sqrt3`

Now,

BC = AC − AB

36 = `CDsqrt3 - (CD)/sqrt3`

36 = `CD (sqrt3 - 1/sqrt3)`

36 = `CD ((sqrt3 xx sqrt3 - 1)/sqrt3)`

36 = `CD ((3 - 1)/sqrt3)`

36 = `CD (2/sqrt3)`

`36 xx sqrt3/2` = CD

`18sqrt3` = CD

CD = `18sqrt3`

CD = 18 × 1.73

CD = 31.14 m

Now,

Height of balloon = DH

= CD + CH

= 31.14 + 1.35

= 32.49 m