Question

O is the point of intersection of two chords AB and CD of a circle.

If ∠BOC = 80° and OA = OD then ΔODA and ΔOBC are ____________.

Options

• equilateral and similar

• isosceles and similar

• isosceles but not similar

• not similar

Answer 1

If ∠BOC = 80° and OA = OD then ΔODA and ΔOBC are isosceles and similar.

Explanation:

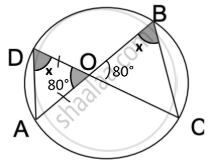
Here, ∠AOD = ∠COB  ...(i) (Vertically opposite angles) 

Also, ∠ODA = ∠OBC  ...(ii) (Angle in the same segment are equal)

Now, In ΔODA and ΔOBC

∠AOD = ∠COB  ...[From (i)]

∠ODA = ∠OBC  ...[From (ii)]

∴ ΔODA ~ ΔOBC  ...(AA similarity)

Since triangles are similar, their sides are proportional

`(OA)/(OC) = (OD)/(OB) = (AD)/(CB)`

For `(OA)/(OC) = (OD)/(OB)`

Putting OD = OA

`(OA)/(OC) = (OA)/(OB)`

OC = OB

Thus, in ΔOBC,

Two sides are equal, so it is isosceles.

Also in ΔODA,

Given OA = OD, two sides are equal, so it is isosceles

Hence, ΔODA and ΔOBC are isosceles and similar.