Question

ABC and DBC are two isosceles triangles on the same side of BC. Prove that:

(i) DA (or AD) produced bisects BC at right angle.

(ii) BDA = CDA.

Answer 1

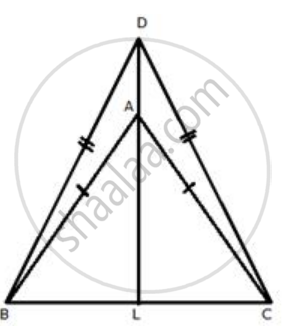
DA is produced to meet BC in L.

In ΔABC,
AB = AC   ...[ Given ]
∴ ∠ACB = ∠ABC.......( i )  ...[ angles opposite to equal sides are equal ]

In ΔDBC, 
DB = DC   ...[ GIven ]
∴ ∠DCB = ∠DBC......( ii )  ...[ angles opposite to equal sides are equal ]

Subtracting (i) from (ii)

∠DCB - ∠ACB = ∠DBC - ∠ABC
⇒ ∠DCA = ∠DBA......( iii )

In ΔDBA and ΔDCA,
DB = DC  ...[ GIven ]
∠DBA = ∠DCA ... [ From ( iii ) ]
AB = AC ...[ Given ]
∴ ΔDBA≅ΔDCA ...[ SAS]
⇒ ∠BDA = ∠CDA.........( iv ) ...[ c. p. c .t ]

In ΔDBA, 
∠BAL = ∠DBA + ∠BDA.......( v ) ...[ Ext. angle = sum opp. int. angles]

From (iii), (iv) and (v)
∠BAL = ∠DCA + ∠CDA.....( v i )

In ΔDCA,, 
∠CAL = ∠DCA + ∠CDA.......( vii ) ...[ Ext. angle = sum opp. int. angles]

From (vi) and (vii)

∠BAL = ∠CAL.......( viii )

In ΔBAL = ΔCAL,
∠BAL = ∠CAL  ...[FROm ( viii ) ] 
∠ABL = ∠ACL   ...[ From ( i ) ]
AB = AC    ...[ Given ]
∴ ΔBAL ΔCAL ...[ ASA]
⇒ ∠ALB = ∠ALC ...{ c. p . c. t ]
and BL = LC........( i x )  ...[ c. p . c .t ]

Now,

 ∠ALB + ∠ALC = 180°
⇒ ∠ALb +  ∠ALB = 180°
⇒ 2∠ALB =180°
⇒ ∠ALB = 90°
∴ AL ⊥ BC
or DL ⊥ BC and BL = LC
∴ DA produced bisects BC at right angle.