Question

In the given figure, AB = AC and ∠DBC = ∠ECB = 90°

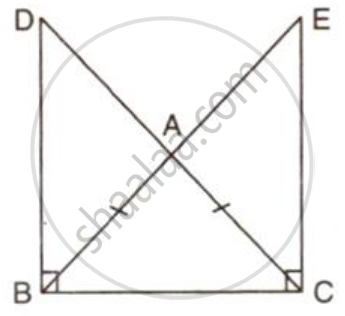
Prove that: 
(i) BD = CE 
(ii) AD = AE

Answer 1

In ΔABC,
AB = AC ......[Given]
∴ ∠ACB = ∠ABC ......[angles opp. to equal sides are equal]
⇒ ∠ABC = ∠ACB .....(i)

∠DBC = ∠ECB = 90° ......[Given]

⇒ ∠DBC = ∠ECB ….(ii)

Subtracting (i) from (ii)
∠DCB − ∠ABC = ∠ECB − ∠ACB
⇒ ∠DBA = ∠ECA ........(iii)

In ΔDBA and ΔECA,
∠DBA = ∠ECA ......[From (iii)]
∠DAB = ∠EAC .......[Vertically opposite angles]
AB = AC ......[Given]
∴ ΔDBA ≅ ΔECA .......[ASA]
⇒ BD = CE ...[c. p. c. t]
Also,
AD = AE ...[c. p. c. t]