Advertisements
Advertisements
Question
ΔABC असा काढा की पाया BC = 3.2 सेमी, ∠ACB = 45° आणि D ABC ची परिमिती 10 सेमी.
Sum
Solution
कच्ची आकृती:
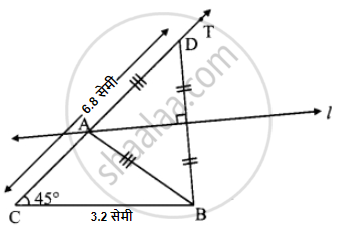
स्पष्टीकरण:
परिमिती Δ ABC = 10 सेमी
⇒ AB + BC + AC = 10 सेमी
10 = AB + 3.2 + AC
AB + AC = 6.8 सेमी
आता, ∆ABC मध्ये,
BC = 3.2 सेमी, ∠ACB = 45° आणि AB + AC = 6.8 सेमी ...(i)
कच्च्या आकृतीत दाखवल्याप्रमाणे BC = 3.2 सेमी हा रेषाखंड प्रथम काढू.
बिंदू C जवळ रेषाखंड CB शी 45° काेन करणाऱ्या किरणावर D बिंदू असा घेऊ की CD = 6.8 सेमी
आता, CA + AD = CD ...[C-A-D]
∴ CA + AD = 6.8 सेमी ...(ii)
AB + AC = 6.8 सेमी ...(iii) [(i) वरून]
∴ CA + AD = AB + AC ...[(i) आणि (ii) वरून]
⇒ AD = AB
बिंदु A हा रेख DB च्या लंबदुभाजकावर आहे.
किरण DB व रेख CT चा लंबदुभाजक यांचा छेदनबिंदू म्हणजे बिंदू A आहे.
रचनेच्या पायऱ्या:
- रेख BC हा 3.2 सेमी काढा.
- C बिंदूपाशी 45° चा कोन करणारा किरण CT काढा.
- किरण CT वर d (C,D) = 6.8 सेमी असा D बिंदू घ्या.
- रेख DB काढा.
- रेख DB चा लंबदुभाजक व किरण CT यांच्या छेदनबिंदूला A नाव द्या.
- रेख AB काढा.
ΔABC हा अपेक्षित त्रिकोण आहे.
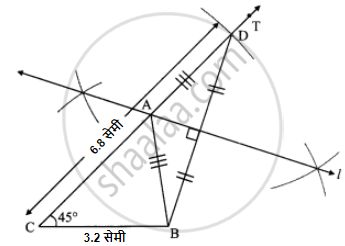
shaalaa.com
त्रिकोण रचना - त्रिकोणाचा पाया, पायालगतचा एक कोन आणि उरलेल्या दोन बाजूंच्या लांबीची बेरीज दिली असता त्रिकोण काढणे.
Is there an error in this question or solution?
