Advertisements
Advertisements
Question
ABCD is a parallelogram, M is the mid-point of BD and BM bisects ∠B. Then ∠AMB =
Options
45°
60°
90°
75°
Solution
Figure is given as follows:
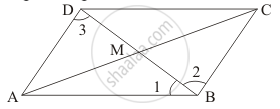
ABCD is a parallelogram.
It is given that :
BM bisects ∠B
Therefore,
∠1 = ∠2
But,
∠2 = ∠3 (Alternate interior opposite angles asDC || AB )
Therefore,
∠1 = ∠3
In ΔABD,
∠1 =∠3
Sides opposite to equal angles are equal.
Thus,
AD = AB
Also,
CD = AB (Opposite sides of a parallelogram are equal)
Thus,
CD = AD
ABCD is a parallelogram with AD = AB
Therefore,
ABCD is a rhombus.
And we know that diagonals of the rhombus bisect each other at right angle.
Thus, ∠AMB = 90°
Hence the correct choice is (c).
APPEARS IN
RELATED QUESTIONS
The angles of quadrilateral are in the ratio 3: 5: 9: 13. Find all the angles of the quadrilateral.
In a parallelogram ABCD, ∠D = 135°, determine the measures of ∠A and ∠B
The following statement are true and false .
In a parallelogram, the diagonals intersect each other at right angles .
The following statement are true and false .
If all the angles of a quadrilateral are equal, it is a parallelogram .
The following statement are true and false .
If three sides of a quadrilateral are equal, it is a parallelogram .
The following statement are true and false .
If three angles of a quadrilateral are equal, it is a parallelogram .
The bisectors of the angle of a parallelogram enclose a
In a parallelogram ABCD, if ∠DAB = 75° and ∠DBC = 60°, then ∠BDC =
ABCD is a parallelogram and E and F are the centroids of triangles ABD and BCDrespectively, then EF =
ABCD is a parallelogram and E is the mid-point of BC. DE and AB when produced meet at F. Then, AF =
