Advertisements
Advertisements
Question
Abdul, while driving to school, computes the average speed for his trip to be 20 km h−1. On his return trip along the same route, there is less traffic and the average speed is 30 km h−1. What is the average speed for Abdul’s trip?
Advertisements
Solution
Let the school be at a distance of x km. If
t1 is the time taken to reach the school, then
`t_1 = "distance"/"average speed" = x/20`
If t2 is the time taken to reach back, then
`t_2 = "distance"/"average speed" = x/30`
Total time,
t = `t_1 + t_2`
= `x/20 + x/30 `
= `x [1/20 + 1/30]`
= `(5x)/60`
= `x/12`
Total distance x + x = 2x
Average speed = `"total distance"/"total time"`
= `(2x)/(x/12)`
= 24 km h-1
APPEARS IN
RELATED QUESTIONS
An aircraft travelling at 600 km/h accelerates steadily at 10 km/h per second. Taking the speed of sound as 1100 km/h at the aircraft’s altitude, how long will it take to reach the ‘sound barrier’ ?
A car is moving along a straight road at a steady speed. It travels 150 m in 5 seconds:
How far does it travel in 1 second ?
A car travels 100 km at a speed of 60 km/h and returns with a speed of 40 km/h. Calculate the average speed for the whole journey.
Write the formula to calculate the speed of a body moving along a circular path. Give the meaning of each symbol which occurs in it.
The diagram below shows the pattern of the oil on the road at a constant rate from a moving car. What information do you get from it about the motion of the car.
A car travels the first 30 km with a uniform speed of 60 km h−1 and the next 30 km with a uniform speed of 40 km h−1. Calculate :
- The total time of journey,
- The average speed of the car.
The velocity-time graph of a moving body is given below in Figure
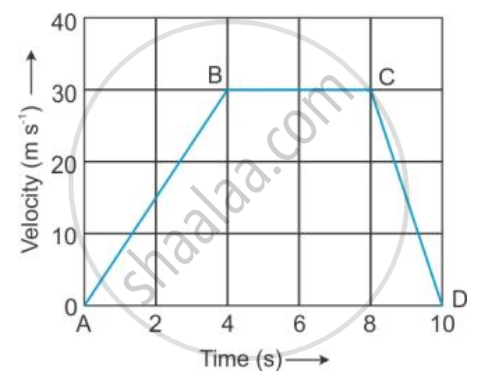
Total displacement.
Draw a diagram to show the motion of a body whose speed remains constant, but velocity changes continuously.
What are the uses of equations of motion?
