Advertisements
Advertisements
Question
Amita wants to make rectangular cards measuring 8 cm × 5 cm. She has a square chart paper of side 60 cm. How many complete cards can she make from this chart? What area of the chart paper will be left?
Solution
The square chart of length 60 cm can be divided exactly in 7 parts each of length 8 cm along one side of chart paper and exactly in 12 parts each of length 5 cm along other side of chart paper.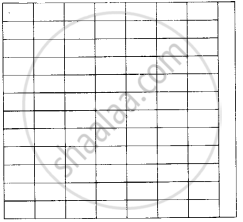
The figure shows that the number of rectangular cards which can be made from the square chart paper is 7 × 12 = 84
Now, area of the square chart paper = (60 × 60) cm2 = 3600 cm2
Area of one rectangular card = (8 × 5) cm2 = 40 cm2
∴ Area of 84 rectangular cards = 84 × 40 cm2 = 3360 cm2
∴ Area of remaining chart paper = (3600 – 3360) cm2 = 240 cm2
APPEARS IN
RELATED QUESTIONS
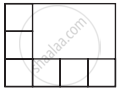
The picture alongside shows some squares. Find out how many squares with the same measures will fit in the empty space in the figure.
The length of the side of a square is given below. Find its area
5 cm
If the cost of 1 sq.m of a plot is ₹ 800, then find the total cost of the plot that is 15 m long and 10 m breadth
its area is ____________ square cm.
Look at these interesting stamps.

Which stamp has the biggest area? How many squares of side 1 cm does this stamp cover? How much is the area of the biggest stamp? square cm.
A wire is cut into several small pieces. Each of the small pieces is bent into a square of side 2 cm. If the total area of the small squares is 28 square cm, what was the original length of the wire?
The area of each square on a chess board is 4sqcm. Find the area of the board.
(a) At the beginning of game when all the chess men are put on the board, write area of the squares left unoccupied.
(b) Find the area of the squares occupied by chess men.
If p squares of each side 1 mm makes a square of side 1 cm, then p is equal to ______.
12 m2 is the area of ______.
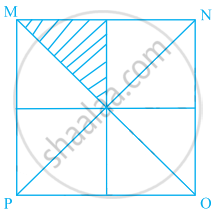
Area of the square MNOP of the given figure is 144 cm2. Area of each triangle is ______.