Advertisements
Advertisements
Question
A wire is cut into several small pieces. Each of the small pieces is bent into a square of side 2 cm. If the total area of the small squares is 28 square cm, what was the original length of the wire?
Solution
Given, side of square made by bending a small piece of wire = 2 cm
And total area of the small squares made by benting small pieces of wire = 28 sq cm
Now, number of small squares = `"Total area of small squares"/"Area of one small squares"`
= `28/(2 xx 2)` ......[∵ Area of square = Side × Side]
= `28/4` = 7
Now, perimeter of a small square = 4 × Side
= 4 × 2
= 8 cm
Perimeter of 7 such small squares = Perimeter of one small square × 7
= 8 × 7
= 56 cm
∴ Original length of wire = Perimeter of 7 small squares = 56 cm
Hence, the original length of wire is 56 cm.
APPEARS IN
RELATED QUESTIONS
Find the breadth of a rectangular plot of land, if its area is 440 m2 and the length is 22 m. Also find its perimeter.
The length of the side of the square is given below. Find its area.
12 metre
The length of the side of the square is given below. Find its area.
25 metres
What will be the area of a new square formed if the side of a square is made one-fourth?
The length of the side of a square is given below. Find its area
16 cm
The length of a rectangular field is 8 m and breadth is 2 m. If a square field has the same perimeter as this rectangular field, find which field has the greater area.
Find the area and Perimeter of the following figure, if area of small square is 1 sq cm.
A square tile of length 20 cm has four quarter circles at each corner as shown in figure (i). Find the area of shaded portion. Another tile with same dimensions has a circle in the centre of the tile in figure (ii). If the circle touches all four sides of the square tile, find the area of the shaded portion. In which tile, area of shaded portion will be more? (Take, π = 3.14)
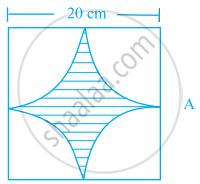 |
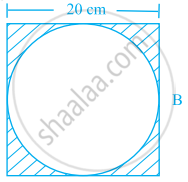 |
| (i) | (ii) |

Calculate the area of shaded region in the given figure, where all of the short line segments are at right angles to each other and 1 cm long.

