Advertisements
Advertisements
Question
Divide the park shown in the figure of question 40 into two rectangles. Find the total area of this park. If one packet of fertilizer is used for 300 sq m, how many packets of fertilizer are required for the whole park?
Solution
Area of rectangle ABCD = Length × Breadth
= (150 × 100) m2
= 15000 m2 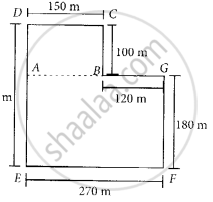
And area of rectangle AGFE = Length × Breadth
= (270 × 180) m2
= 48600 m2
∴ Total area of the park = 15000 m2 + 48600 m2
= 63600 m2
Number of packets of fertilizer used for 300 m2 = 1
∴ Number of packets of fertilizer used for 63600 m2 = `63600/300` = 212
APPEARS IN
RELATED QUESTIONS
A rectangular hall is 12 m long and 6 m broad. Its flooring is to be made of square tiles of side 30 cm. How many tiles will fit in the entire hall? How many would be required if tiles of side 15 cm were used?
What will be the labour cost of laying the floor of an assembly hall that is 16 m long and 12 m wide if the cost of laying 1 sq m is 80 rupees?
What will be the labour cost of laying the floor of an assembly hall which is 14 m long and 10 m breadth if the cost of laying is ₹ 60 per sq.m?
Find the area of the rectangle whose sides are:
3 cm and 4 cm
The length and breadth of the three rectangles are as given below:
- 9 m and 6 m
- 17 m and 3 m
- 4 m and 14 m
Which one has the largest area and which one has the smallest?
What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of ₹ 8 per hundred sq m.?
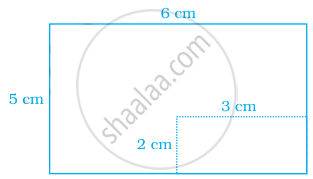
A rectangular piece of dimensions 3 cm × 2 cm was cut from a rectangular sheet of paper of dimensions 6 cm × 5 cm (see the figure). Area of remaining sheet of paper is ______.
The perimeter of a rectangle is 40 m. Its length is four metres less than five times its breadth. Find the area of the rectangle.
A wall of a room is of dimensions 5 m × 4 m. It has a window of dimensions 1.5 m × 1 m and a door of dimensions 2.25 m × 1 m. Find the area of the wall which is to be painted.
4 squares each of side 10 cm have been cut from each corner of a rectangular sheet of paper of size 100 cm × 80 cm. From the remaining piece of paper, an isosceles right triangle is removed whose equal sides are each of 10 cm length. Find the area of the remaining part of the paper.
