Advertisements
Advertisements
Question
An ac circuit consists of a series combination of circuit elements X and Y. The current is ahead of the voltage in phase by `pi /4` . If element X is a pure resistor of 100Ω ,
(a) name the circuit element Y.
(b) calculate the rms value of current, if rms value of voltage is 141V.
(c) what will happen if the ac source is replaced by a dc source ?
Solution
(a) Since current is leading voltage by `pi/4`, current leak in capacitive curcuit as X is pure resistor therefore Y capacitor.
(b) `phi = tan ^(-1) ((X_c - X_L)/R) X_L = 0`
`pi/4 = tan^(-1)((X_c)/R)`
`(X_c)/R= tan pi/4`
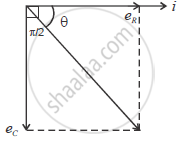
`(X_c)/R= 1` Xc = R
Xc = 100 Ω
`t = sqrt((100)^2 + (100)^2)`
`t = 100 sqrt(2) Omega = 100 xx 1.41 = 141 Omega `
`i_(RMS) = (e_(RMS))/z = 141/141 = 1A`
iRMS = 1A
(c) If we replace ac source by dc ω = 0
`X_c = 1/(omega _c)`
`X_c = 1/0 = ∞ Omega`
`i = e/z = 141/ ∞ `
i = 0
APPEARS IN
RELATED QUESTIONS
Three capacitors each of capacitance 9 pF are connected in series.
- What is the total capacitance of the combination?
- What is the potential difference across each capacitor if the combination is connected to a 120 V supply?
Deduce an expression for equivalent capacitance C when three capacitors C1, C2 and C3 connected in parallel.
A parallel-plate capacitor having plate area 20 cm2 and separation between the plates 1⋅00 mm is connected to a battery of 12⋅0 V. The plates are pulled apart to increase the separation to 2⋅0 mm. (a) Calculate the charge flown through the circuit during the process. (b) How much energy is absorbed by the battery during the process? (c) Calculate the stored energy in the electric field before and after the process. (d) Using the expression for the force between the plates, find the work done by the person pulling the plates apart. (e) Show and justify that no heat is produced during this transfer of charge as the separation is increased.
A capacitor of capacitance 5⋅00 µF is charged to 24⋅0 V and another capacitor of capacitance 6⋅0 µF is charged to 12⋅0 V. (a) Find the energy stored in each capacitor. (b) The positive plate of the first capacitor is now connected to the negative plate of the second and vice versa. Find the new charges on the capacitors. (c) Find the loss of electrostatic energy during the process. (d) Where does this energy go?
Three different capacitors are·connected in series. Then:-
The total charge on the system of capacitors C1 = 1 µF, C2 = 2 µF, C3 = 4 µF and C4 = 3 µF connected in parallel is ______. (Assume a battery of 20 V is connected to the combination)
The capacitors, each of 4 µF are to be connected in such a way that the effective capacitance of the combination is 6 µF. This can be achieved by connecting ______.
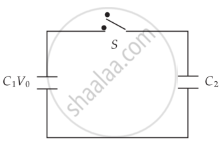
A capacitor of capacity C1 is charged to the potential of V0. On disconnecting with the battery, it is connected with an uncharged capacitor of capacity C2 as shown in the adjoining figure. Find the ratio of energies before and after the connection of switch S.
Three capacitors of capacitances 2 pF, 3 pF and 4 pF are connected in parallel. What is the total capacitance of the combination?
