Advertisements
Advertisements
Question
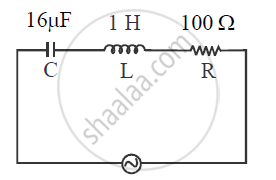
An A.C. generator generating an emf of ε = 300 sin (100 πt) V is connected to a series combination of 16μ F capacitor, 1 H inductor and 100 Ω resistor.
Calculate :
1) An impedance of the circuit at the given frequency.
2) Resonant frequency `f_0`
3)Power factor at the resonant frequency `f_0`.
Solution
`E = 300sin(100pit)`
C = capacitor = `16muF`
L = Inductar = 1H
`E = 300sin(100pit)`
From `E = 300 sin (100pit)`
`omega = 100 pi`
`2pif = 100pi`
`:. f = 50 Hz`
`:. X_C =1/(2pifC) = 1/(2pixx50xx16xx10^(-6))= 1/(5026.5 xx 10^(-6)) = 1.98 xx 10^(-4) xx 10^6`
`:. X_C = 198 Ω`
`X_L = 2pifl = 2pi xx 50 xx 1 = 3.14.1 Ω`
1) Impedence of the circuit (Z
`Z = sqrt(R^2 + (X_L -X_C)^2) `
`= [(100)^2 + (314 - 198 )^2]^("1/2")`
= 153.15 Ω
2) Resonant frequency `(f_0)`
`f_0 = 1/(2pisqrt(LC))`
`= 1/(2pisqrt(1xx16xx10^(-6)))`
= 39.84 Hz
3) at Resonance `X_C = X_L`
`:. Z =R`
`cos phi = R/Z`
`cos phi = R/R`
`cos phi = 1`
`"power factor" (cos phi) = 1`
APPEARS IN
RELATED QUESTIONS
An a.c. source of voltage V = V0 sin ωt is connected to a series combination of L, C, and R. Use the phasor diagram to obtain the expression for an impedance of a circuit and the phase angle between voltage and current. Find the condition when current will be in phase with the voltage. What is the circuit in this condition called?
When an AC source is connected to an ideal inductor show that the average power supplied by the source over a complete cycle is zero.
Ajit had a high tension tower erected on his farm land. He kept complaining to the authorities to remove it as it was occupying a large portion of his land. His uncle, who was a teacher, explained to him the need for erecting these towers for efficient transmission of power. As Ajit realised its significance, he stopped complaining.
Answer the following questions:
(a) Why is it necessary to transport power at high voltage?
(b) A low power factor implies large power loss. Explain.
(c) Write two values each displayed by Ajit and his uncle.
For a given a.c., i = im sin ωt, show that the average power dissipated in a resistor R over a complete cycle is `1/2I_m^2` R .
A series AC circuit has a resistance of 4 Ω and a reactance of 3 Ω. The impedance of the circuit is
Transformers are used ______.
In an AC series circuit, the instantaneous currt is zero when the instantaneous voltage is maximum. Connected to the source may be a
(a) pure inductor
(b) pure capacitor
(c) pure resistor
(d) combination of an inductor and a capacitor
The current in a discharging LR circuit is given by i = i0 e−t/τ , where τ is the time constant of the circuit. Calculate the rms current for the period t = 0 to t = τ.
The power factor of an a.c circuit having resistance R and inductance L Connected in series to an a.c source of angular frequency co is.
In the series LCR circuit, the power dissipation is through ______
