Advertisements
Advertisements
Question
An electron of kinetic energy 100 eV circulates in a path of radius 10 cm in a magnetic field. Find the magnetic field and the number of revolutions per second made by the electron.
Solution
Given:
Kinetic energy of an electron = 100 eV
Radius of the circle = 10 cm
`1/2mv^2` = 100 eV = 1.6 × 10−17 J (1 eV = 1.6 × 10−19 J)
Here,
m is the mass of an electron and v is the speed of an electron. Thus,
1/2 × 9.1 × 10−31 × v2 = 1.6 × 10−17 J
⇒ v2 = 0.35 × 1014
v = 0.591 × 107 m/s
Now,
`r = (mv)/(eB)`
`⇒ B = (mv)/(er)`
`= (9.1xx10^-31xx0.591xx10^7)/(1.6xx10^-19xx0.1)`
B = 3.3613 × 10−4 T
Therefore, the applied magnetic field = 3.4 × 10−4 T
Number of revolutions per second of the electron,
`f = 1/T`
`T = (2pir)/v= 2pim/(eB)`
`T = (2pim)/Be`
`f = (Be)/(2pim)`
`=( 3.4xx10^-4xx1.6xx10^-19)/(2xx3.14xx9.1xx10^-31`
= 0.094 × 108
= 9.4 × 106
f = 9.4 × 106
APPEARS IN
RELATED QUESTIONS
A moving charged particle q travelling along the positive x-axis enters a uniform magnetic field B.
When will the force acting on q be maximum?
A proton and an α-particle move perpendicular to a magnetic field. Find the ratio of radii of circular paths described by them when both have (i) equal velocities, and (ii) equal kinetic energy.
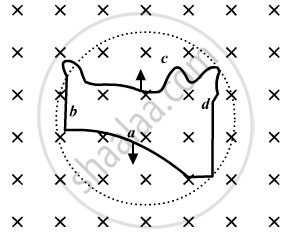
A flexible wire of irregular shape, abcd, as shown in the figure, turns into a circular shape when placed in a region of magnetic field which is directed normal to the plane of the loop away from the reader. Predict the direction of the induced current in the wire.
A charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be
An electric current i enters and leaves a uniform circular wire of radius a through diametrically opposite points. A charged particle q, moving along the axis of the circular wire, passes through its centre at speed v. The magnetic force acting on the particle, when it passes through the centre, has a magnitude equal to
If a charged particle moves unaccelerated in a region containing electric and magnetic fields
(a) `vecE "must be perpendicular" to vecB`
(b) `vecv "must be perpendicular" to vecE`
(c) must be perpendicular to v_B
Two ions have equal masses but one is singly-ionised and the other is doubly-ionised. They are projected from the same place in a uniform magnetic field with the same velocity perpendicular to the field.
(a) Both ions will move along circles of equal radii.
(b) The circle described by the singly-ionised charge will have a radius that is double that of the other circle.
(c) The two circles do not touch each other.
(d) The two circles touch each other.
A particle is projected in a plane perpendicular to a uniform magnetic field. The area bounded by the path described by the particle is proportional to
An experimenter's diary reads as follows: "A charged particle is projected in a magnetic field of `(7.0 vec i - 3.0 vecj)xx 10^-3 `T. The acceleration of the particle is found to be `(x veci + 7.0 vecj )` The number to the left of i in the last expression was not readable. What can this number be?
A wire, carrying a current i, is kept in the x−y plane along the curve y = A sin `((2x)/lamda x)`. magnetic field B exists in the z direction. Find the magnitude of the magnetic force on the portion of the wire between x = 0 and x = λ.
A proton describes a circle of radius 1 cm in a magnetic field of strength 0.10 T. What would be the radius of the circle described by an α-particle moving with the same speed in the same magnetic field?
A circular coil of radius 2.0 cm has 500 turns and carries a current of 1.0 A. Its axis makes an angle of 30° with the uniform magnetic field of magnitude 0.40 T that exists in the space. Find the torque acting on the coil.
A square coil of edge l and with n turns carries a current i. It is kept on a smooth horizontal plate. A uniform magnetic field B exists parallel to an edge. The total mass of the coil is M. What should be the minimum value of B for which the coil will start tipping over?
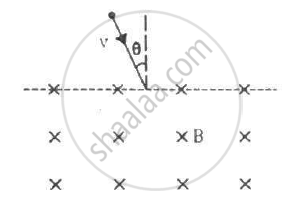
A particle of mass m and positive charge q, moving with a uniform velocity v, enters a magnetic field B, as shown in the figure. (a) Find the radius of the circular arc it describes in the magnetic field. (b) Find the angle subtended by the arc at the centre. (c) How long does the particle stay inside the magnetic field? (d) Solve the three parts of the above problem if the charge q on the particle is negative.
The figure shows a convex lens of focal length 12 cm lying in a uniform magnetic field Bof magnitude 1.2 T parallel to its principal axis. A particle with charge 2.0 × 10−3 C and mass 2.0 × 10−5 kg is projected perpendicular to the plane of the diagram with a speed of 4.8 m s−1. The particle moves along a circle with its centre on the principal axis at a distance of 18 cm from the lens. Show that the image of the particle moves along a circle and find the radius of that circle.

A uniform magnetic field of magnitude 0.20 T exists in space from east to west. With what speed should a particle of mass 0.010 g and with charge 1.0 × 10−5 C be projected from south to north so that it moves with uniform velocity?
A particle of mass m and charge q is released from the origin in a region in which the electric field and magnetic field are given by
`vecB = -B_0 vecj and vecE = E_0 vecK `
Find the speed of the particle as a function of its z-coordinate.
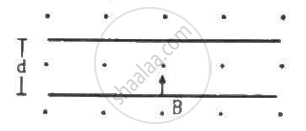
An electron is emitted with negligible speed from the negative plate of a parallel-plate capacitor charged to a potential difference V. The separation between the plates is dand a magnetic field B exists in the space, as shown in the figure. Show that the electron will fail to strike the upper plates if `d > ((2m_eV)/(eB_0^2))^(1/2)`
The velocity of a body of mass 2 kg as a function of time t is given by v(t) = 2t`hat"i" + "t"^2hat"j"`. The force acting on it, at time t = 2 s is given by ______.
A particle of mass 10 mg and having a charge of 50 mC is projected with a speed of 15 m/s into a uniform magnetic field of 125 mT. Assuming that the particle is projected with its velocity perpendicular to the magnetic field, the time after which the particle reaches its original position for the first time is ______.
