Advertisements
Advertisements
Question
An element with molar mass 27 g/mol forms a cubic unit cell with edge length of 405 pm. If the density of the element is 2.7 g/cm3, what is the nature of the cubic unit cell?
Solution
Given:
Edge length (a) = 405 pm = 4.05 × 10-8 cm
Molar mass = 27 g mol-1,
Density (ρ) = 2.7 g/cm3 = 2.7 g cm−3
To find: Nature of cubic unit cell
Formula: Density (ρ) = `(M n)/(a^3 N_A)`
Calculation: From the formula,
Density, ρ = `(M n)/(a^3 N_A)`
∴ `2.7 "g cm"^-3 = (27 "g mol"^-1 xx "n")/((4.05 xx 10^-8)^3 "cm"^3 xx 6.022 xx 10^23 "atom mol"^-1)`
∴ n = `(2.7 "g cm"^-3 xx (4.05 xx 10^-8)^3 "cm"^3 xx 6.022 xx 10^23 "atom mol"^-1)/(27 "g mol"^-1)`
= 4.00
∴ Number of atoms in unit cell = 4
Since unit cell contains 4 atoms, it has face-centred cubic (fcc) or ccp structure.
The nature of the given cubic unit cell is face-centred cubic (fcc) or ccp unit cell.
RELATED QUESTIONS
Obtain the relationship between the density of a substance and the edge length of the unit cell.
Give the percentage of empty space in bcc lattice.
An element (atomic mass M g/mol) having bcc structure has unit cell edge 400 pm. The density of the element is ____________ g/cm3.
[NA = 6.0 × 1023 atom mol−1)
The percentage of unoccupied volume in simple cubic cell is ______.
The number of atoms in 500 g of a fcc crystal of a metal with density d = 10 g/cm3 and cell edge 100 pm, is equal to ____________.
A metal crystallises in bcc unit cell with edge length 'a'. What will be the volume of one atom?
Sodium crystallizes in bcc structure with radius 1.86 × 10−8 cm. What is the length of unit cell of sodium?
An element crystallizes bcc type of unit cell, the density and edge length of unit cell is 4 g cm−3 and 500 pm respectively. What is the atomic mass of an element?
An element with density 2.8 g cm−3 forms fcc unit cell having edge length 4 × 10−8 cm. Calculate molar mass of the element.
Copper and silver have ____________ crystal structure.
Consider the following unit cell.
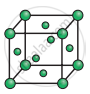
The number of particles (spheres) per unit cell is:
A metallic element has a cubic lattice with edge length of unit cell 2 Å. Calculate the number of unit cells in 200 g of the metal, if density of metal is 2.5 g cm-3?
Which of the following formulae is used to find edge length of bee unit cell?
Gold crystallises into face-centred cubic cells. The edge length of a unit cell is 4.08 × 10–8 cm. Calculate the density of gold. [Molar mass of gold = 197 g mol–1]
A metal has an fcc lattice. The edge length of the unit cell is 404 pm. The density of the metal is 2.72 g cm−3. The molar mass of the metal is ______.
(NA Avogadro's constant = 6.02 × 1023 mol−1)
Calculate the density of metal with molar mass 56 g mol- 1 that crystallises to form a bcc structure with edge length 288 pm.
Identify unit cell from following having four particles in it
What is the density of potassium, if it has a bcc structure with edge length 4Å?
(Atomic mass of K = 39)
Silver crystallizes in the fcc structure. If the edge length of the unit cell is 400 pm, calculate the density of silver (Atomic mass of Ag = 108).
The correct sequence of the atomic layers in cubic close packing is ______.
The total number of different primitive unit cells is ______.
What would be the empirical formula of a compound having a unit cell containing A ion shared equally at the corner of the cube and B ion on the centre of faces of the cube?
