Advertisements
Advertisements
Question
An ice cream pot has a right circular cylindrical shape. The radius of the base is 12 cm and the height is 7 cm. This pot is completely filled with ice cream. The entire ice cream is given to the students in the form of right circular ice cream cones, having a diameter of 4 cm and a height is 3.5 cm. If each student is given one cone, how many students can be served?
Solution
Cylinder:
Radius = 12 cm
Height = 7 cm
Cone:
Diameter = 4 cm
Radius = 2 cm
Height = 3.5 cm
Let there be n students.
n × Volume of cone = Volume of cylinder
`"n" xx 1/3π"r"^2"h" = π"r"^2"H"`
`"n"/3 xx 2 xx 2 xx 3.5 = 12 xx 12 xx 7`
n = `(12 xx 12 xx 3)/2`
n = 12 × 18
n = 216 students
APPEARS IN
RELATED QUESTIONS
Water flows at the rate of 15 m per minute through a cylindrical pipe, having the diameter 20 mm. How much time will it take to fill a conical vessel of base diameter 40 cm and depth 45 cm?
A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank which is 10 m in diameter and 2 m deep. If the water flows through the pipe at the rate of 4 km per hour, in how much time will the tank be filled completely?
A toy is a combination of a cylinder, hemisphere and a cone, each with radius 10 cm as shown in the figure. Height of the conical part is 10 cm and total height is 60 cm. Find the total surface area of the toy.
(π=3.14, √2=1.41)
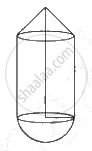
A cylinder and a cone have equal bases. The height of the cylinder is 3 cm and the area of its base is 100 cm2. The cone is placed upon the cylinder. The volume of the solid figure so formed is 500 cm3. Find the total height of the figure.

In the given figure, a toy made from a hemisphere, a cylinder and a cone are shown. Find the total area of the toy.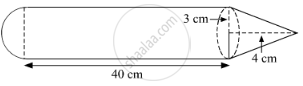
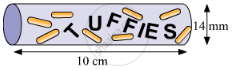
In the given figure, a cylindrical wrapper of flat tablets is shown. The radius of a tablet is 7 mm and its thickness is 5 mm. How many such tablets are wrapped in the wrapper?
In the given figure shows a toy. Its lower part is a hemisphere and the upper part is a cone. Find the volume and surface area of the toy from the measures shown in the figure (\[\pi = 3 . 14\])
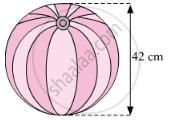
Find the surface area and the volume of a beach ball shown in the figure.
A tin maker converts a cubical metallic box into 10 cylindrical tins. The side of the cube is 50 cm and the radius of the cylinder is 7 cm. Find the height of each cylinder so made, if the wastage of 12% is incurred in the process `(pi = 22/7)`
A vessel is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter is 14 cm and the height of the vessel is 13 cm. Find the capacity of the vessel
Nathan, an engineering student was asked to make a model shaped like a cylinder with two cones attached at its two ends. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of the model that Nathan made.
From a solid cylinder whose height is 2.4 cm and the diameter 1.4 cm, a cone of the same height and same diameter is carved out. Find the volume of the remaining solid to the nearest cm3.
A solid consisting of a right circular cone of height 12 cm and radius 6 cm standing on a hemisphere of radius 6 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of the water displaced out of the cylinder, if the radius of the cylinder is 6 cm and height is 18 cm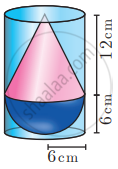
A right circular cylinder just encloses a sphere of radius r units. Calculate the curved surface area of the cylinder
A hollow metallic cylinder whose external radius is 4.3 cm and internal radius is 1.1 cm and the whole length is 4 cm is melted and recast into a solid cylinder of 12 cm long. Find the diameter of a solid cylinder
Find volume of solid generated by revolving parabola y2. = 4ax, cut of by latus rectum, about tangent at vertex.
A right circular cylinder which is open at the top and has a given surface area, will have the greatest volume if its height h and radius r are related by
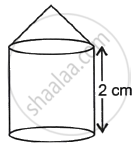
A cylinder and a cone have equal bases. The height of the cylinder is 2 cm and the area of its base is 64 cm2. The cone is placed upon the cylinder volume of the solid figure so formed is 400 cm3. Find the total height of the figure.