Advertisements
Advertisements
Question
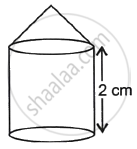
From a solid cylinder whose height is 2.4 cm and the diameter 1.4 cm, a cone of the same height and same diameter is carved out. Find the volume of the remaining solid to the nearest cm3.
Solution
Radius of a cylinder = Radius of a cone (r) = 0.7 cm
Height of a cylinder = Height of a cone (h) = 2.4 cm
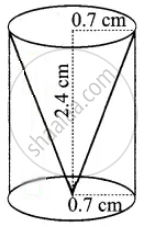
Volume of the remaining solid = Volume of the cylinder – Volume of a cone
= `pi"r"^2"h" - 1/3 pi"r"^2"h" "cm"^3`
= `pi"r"^2"h" (1 - 1/3) "cm"^3`
= `22/7 xx 0.7 xx 0.7 xx 2.4 xx 2/3 "cm"^3`
= `22/7 xx 7/10 xx 7/10 xx 24/10 xx 2/3 "cm"^3`
= `(22 xx 7 xx 24 xx 2)/(1000 xx 3) "cm"^3`
= `(22 xx 7 xx 8 xx 2)/(1000) "cm"^3`
= 2.464 cm3
= 2.46 cm3
Volume of the remaining soild = 2.46 cm3
Notes
APPEARS IN
RELATED QUESTIONS
Water flows at the rate of 15 m per minute through a cylindrical pipe, having the diameter 20 mm. How much time will it take to fill a conical vessel of base diameter 40 cm and depth 45 cm?
A toy is a combination of a cylinder, hemisphere and a cone, each with radius 10 cm as shown in the figure. Height of the conical part is 10 cm and total height is 60 cm. Find the total surface area of the toy.
(π=3.14, √2=1.41)

Observe the measures of pots In the given figure. How many jugs of water can the cylindrical pot hold?
In the given figure shows a toy. Its lower part is a hemisphere and the upper part is a cone. Find the volume and surface area of the toy from the measures shown in the figure (\[\pi = 3 . 14\])
A vessel is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter is 14 cm and the height of the vessel is 13 cm. Find the capacity of the vessel
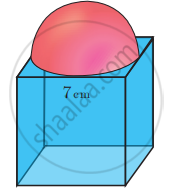
As shown in the figure a cubical block of side 7 cm is surmounted by a hemisphere. Find the surface area of the solid.
A right circular cylinder just encloses a sphere of radius r units. Calculate the surface area of the sphere
Suppose we have block of 4 kilogram kept on a horizontal surface and we are applying a horizontal force of 10 newton. Let the coefficient of friction is 0.2. Find the force of friction. Assume that g = 10.
Find volume of solid generated by revolving parabola y2. = 4ax, cut of by latus rectum, about tangent at vertex.
A cylinder and a cone have equal bases. The height of the cylinder is 2 cm and the area of its base is 64 cm2. The cone is placed upon the cylinder volume of the solid figure so formed is 400 cm3. Find the total height of the figure.