Question

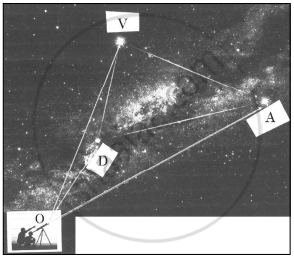
An instructor at the astronomical centre shows three among the brightest stars in a particular constellation. Assume that the telescope is located at O (0,0,0) and the three stars have their locations at the points D, A and V having position vectors `2hati+3hatj+4hatk, 7hati+5hatj+8hatk and -3hati+7hatj+11hatk` respectively.

Based on the above information, answer the following questions:

(i) How far is the star V from star A?  (1)

(ii) Find a unit vector in the direction of `vec(DA)`.  (1)

(iii) Find the measure of ∠VDA.  (2)

OR

(iii) What is the projection of vector `vec(DV)  "on vector"  vec(DA)`  (2)

Answer 1

(i) Distance between VA

`vec(VA)` = P.V. of A − P.V. of V

`= (7hati+5hatj+8hatk)-(-3hati+7hatj+11hatk)`

`vec(VA) = 10hati-2hatj-3hatk`

`|vec(VA)| = sqrt(100+4+9) = sqrt113`

(ii) Unit vector in direction `vec(DA)`

`= vec(DA)/|vec(DA)|`

`vec(DA)` = P.V of A − P.V of D

`= (7hati+5hatj+8hatk)-(2hati+3hatj+4hatk)`

`vec(DA) = 5hati+2hatj+4hatk`

unit vector = `(5hati+2hatj+4hatk)/sqrt(25+4+16)`

= `(5hati+2hatj+4hatk)/sqrt45`

(iii) Angle of ∠VDA

Let `vec(DA) = veca`

`vec(DV) = vecb`

So, `veca=5hati+2hatj+4hatk`

`vecb=-5hati+4hatj+7hatk`

Angle `cos theta=(veca.vecb)/(|veca| |vecb|)`

`= (-25+8+28)/(sqrt(25+4+16) sqrt(25+16+49))`

`costheta = 11/(sqrt45sqrt90)=11/(45sqrt2)`

`theta = cos^-1 (11/(45sqrt2))`

OR

(iii) Projection of vector `vec(DV)` on vector `vec(DA)`

`=(vec(DV).vec(DA))/|vec(DA)|`

`= 11/sqrt45`