Commerce (English Medium)
Science (English Medium)
Arts (English Medium)
Academic Year: 2023-2024
Date & Time: 9th March 2024, 10:30 am
Duration: 3h
Advertisements
General Instructions:
Read the following instructions very carefully and strictly follow them:
- This Question paper contains 38 questions. All questions are compulsory.
- Question paper is divided into FIVE Sections - Section A, B, C, D and E.
- In Section A - Questions Number 1 to 18 are Multiple Choice Questions (MCQs) type and Questions Number 19 & 20 are Assertion-Reason based questions of 1 mark each.
- In Section B - Questions Number 21 to 25 are Very Short Answer (VSA) type questions, carrying 2 marks each.
- In Section C - Questions Number 26 to 31 are Short Answer (SA) type questions, carrying 3 marks each.
- In Section D - Questions Number 32 to 35 are Long Answer (LA) type questions, carrying 5 marks each.
- In Section E - Questions Number 36 to 38 are case study based questions, carrying 4 marks each.
- There is no overall choice. However, an internal choice has been provided in 2 questions in Section - B, 3 questions in Section - C, 2 questions in Section - D and 2 questions in Section - E.
- Use of calculators is NOT allowed.
The lines `(1-x)/2=(y-1)/3=z/1` and `(2x-3)/(2p)=(y)/-1=(z-4)/7` are perpendicular to each other for p equal to ______.
`-1/2`
`1/2`
2
3
Chapter:
The maximum value of Z = 4x + y for a L.P.P. whose feasible region is given below is ______.

50
110
120
170
Chapter:
The probability distribution of a random variable X is:
| X | 0 | 1 | 2 | 3 | 4 |
| P(X) | 0.1 | k | 2k | k | 0.1 |
where k is some unknown constant.
The probability that the random variable X takes the value 2 is ______.
`1/5`
`2/5`
`4/5`
1
Chapter:
If A = [aij] = `[(2,-1,5),(1,3,2),(5,0,4)]` and cij is the cofactor of element aij, then the value of a21 × c11 + a22 × c12 + a23 × c13 is ______.
−57
0
9
57
Chapter:
If A `= [(1,3),(3,4)]` and A2 − kA − 5I = 0, then the value of k is ______.
5
3
7
9
Chapter: [0.03] Matrices
If `e^(x^2y)` = c, then `dy/dx` is ______.
`(xe^(x^2y))/(2y)`
`(-2y)/x`
`(2y)/x`
`x/(2y)`
Chapter:
The value of constant c that makes the function f defined by
`f(x) = {{:(x^2-c^2; if x < 4),(cx+20 ; if x > 4):}`
continuous for all real numbers is ______.
−2
−1
0
2
Chapter:
The number of arbitrary constants in the particular solution of the differential equation `log (dy/dx) = 3x+4y; y(0) = 0` is/are ______.
2
1
0
3
Chapter:
If `[(a,c,0),(b,d,0),(0,0,5)]` is a scalar matrix, then the value of a + 2b + 3c + 4d is ______.
0
5
10
25
Chapter:
If A = `[(2,1),(-4,-2)]`, then the value of I – A + A2 – A3 + ... is ______.
`[(-1,-1),(4,3)]`
`[(3,1),(-4,-1)]`
`[(0,0),(0,0)]`
`[(1,0),(0,1)]`
Chapter:
Given that A-1= `1/7 [(2,1),(-3,2)]`, matrix A is ______.
`7 [(2,-1),(3,2)]`
`[(2,-1),(3,2)]`
`1/7 [(2,-1),(3,2)]`
`1/49 [(2,-1),(3,2)]`
Chapter:
The integrating factor of the differential equation `(x+2y^2) dy/dx = y (y>0)` is ______.
`1/x`
x
y
`1/y`
Chapter:
A vector perpendicular to the line `vecr=hati+hatj-hatk+λ(3hati-hatj)` is ______.
`5hati+hatj+6k`
`hati+3hatj+5hatk`
`2hati-2hatj`
`9hati-3hatj`
Chapter:
The vectors `\veca= 2hati - hatj + hatk, \vecb = hati - 3hatj - 5hatk and \vecc = -3hati + 4hatj +4hatk` represents the sides of ______.
an equilateral triangle
an obtuse-angled triangle
an isosceles triangle
a right-angled triangle
Chapter:
Let `veca` be any vector such that `|veca| = a`. The value of `|vecaxxhati|^2 + |vecaxxhatj|^2 + |vecaxxhatk|^2` is ______.
a2
2a2
3a2
0
Chapter:
If `veca` and `vecb` are two vectors such that `|vec{a}| = 1, |vec{b}| = 2 and vec{a}.vec{b} = root 3,` then the angle between `2vec{a} and vec{-b}` is ______.
`pi/6`
`pi/3`
`(5pi)/6`
`(11pi)/6`
Chapter:
The function f(x) = kx – sin x is strictly increasing for ______.
k > 1
k < 1
k > –1
k < –1
Chapter:
Advertisements
Assertion (A): The corner points of the bounded feasible region of a L.P.P. are shown below. The maximum value of Z = x + 2y occurs at infinite points.
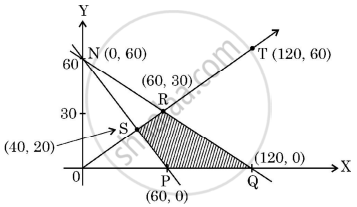
Reason (R): The optimal solution of a LPP having bounded feasible region must occur at corner points.
Both Assertion (A) and Reason (R) are true and the Reason (R) is the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true and Reason (R) is not the correct explanation of the Assertion (A).
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Chapter:
Assertion(A): The relation R = {(x,y) : (x +y) is a prime number and x, y ∈ N} is not a reflexive relation.
Reason (R): The number ‘2n’ is composite for all natural numbers n.
Both Assertion (A) and Reason (R) are true and the Reason (R) is the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true and Reason (R) is not the correct explanation of the Assertion (A).
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Chapter:
The volume of a cube is increasing at the rate of 6 cm3/s. How fast is the surface area of cube increasing, when the length of an edge is 8 cm?
Chapter:
Express `tan^-1(cos x/(1-sin x)), "where" (-pi)/2 <x<pi/2` in the simplest form.
Chapter:
Find the principal value of `tan^-1(1)+cos^-1(-1/2)+sin^-1(-1/root 2)`.
Chapter:
Show that `f(x) =(4 sinx)/(2+cosx) -x` is an increasing function of x in `[0, pi/2]`
Chapter:
If `x^y = e^(x-y), "prove that" dy/dx = logx/(1 + log x)^2`.
Chapter:
Evaluate:
`int_(-1/2)^(1/2) cosx.log ((1+x)/(1-x))dx`
Chapter:
Given that xy + yx = ab, where a and b are positive constants, find `dy/dx`.
Chapter:
Find the particular solution of the differential equation `dy/dx = y cot 2x`, given that `y(pi/4) = 2.`
Chapter:
Find the particular solution of the differential equation `(xe^(y/x) +y) dx = x dy,` given that y = 1 when x = 1.
Chapter:
A card from a well shuffled deck of 52 playing cards is lost. From the remaining cards of the pack, a card is drawn at random and is found to be a King. Find the probability of the lost card being a King.
Chapter:
Advertisements
A biased die is twice as likely to show an even number as an odd number. If such a die is thrown twice, find the probability distribution of the number of sixes. Also, find the mean of the distribution.
Chapter:
Solve the following L.P.P. graphically:
Maximise Z = x + 3y
subject to the constraints:
x + 2y ≤ 200
x + y ≤ 150
y ≤ 75
x, y ≥ 0
Chapter:
Evaluate:
`int_0^(pi/4) (x dx)/(1+cos2x+sin2x)`
Chapter:
Find:
`inte^x [1/(1+x^2)^(3/2) + x/(sqrt (1+x^2))] dx`
Chapter:
Let A = R – {5} and B = R – {1}. Consider the function f : A → B, defined by `f(x) = (x-3)/(x-5)`. Show that f is one-one and onto.
Chapter:
Check whether the relation S in the set of real numbers R defined by S = {(a, b): where a – b + `sqrt2` is an irrational number} is reflexive, symmetric or transitive.
Chapter:
Find the distance between the line `x/2 = (2y-6)/4 = (1-z)/-1` and another line parallel to it passing through the point (4, 0, −5).
Chapter:
If the lines `(x-1)/-3=(y-2)/(2k)=(z-3)/2 and (x-1)/(3k)=(y-1)/1=(z-6)/-7` are perpendicular to each other, find the value of k and hence write the vector equation of a line perpendicular to these two lines and passing through the point (3, –4, 7).
Chapter:
Use the product of matrices `[(1,2,-3),(3,2,-2),(2,-1,1)][(0,1,2),(-7,7,-7),(-7,5,-4)]` to solve the following system of equations:
x + 2y – 3z = 6
3x + 2y – 2z = 3
2x – y + z = 2
Chapter:
Sketch the graph of y = x |x| and hence find the area bounded by this curve, X-axis and the ordinates x = –2 and x = 2, using integration.
Chapter:
Using integration, find the area bounded by the ellipse 9x2 + 25y2 = 225, the lines x = –2, x = 2, and the X-axis.
Chapter:
|
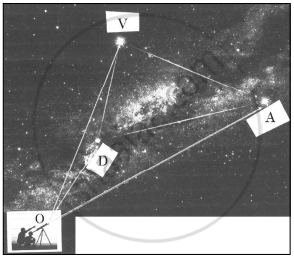
An instructor at the astronomical centre shows three among the brightest stars in a particular constellation. Assume that the telescope is located at O (0,0,0) and the three stars have their locations at the points D, A and V having position vectors `2hati+3hatj+4hatk, 7hati+5hatj+8hatk and -3hati+7hatj+11hatk` respectively.
|
Based on the above information, answer the following questions:
(i) How far is the star V from star A? (1)
(ii) Find a unit vector in the direction of `vec(DA)`. (1)
(iii) Find the measure of ∠VDA. (2)
OR
(iii) What is the projection of vector `vec(DV) "on vector" vec(DA)` (2)
Chapter:
|
Rohit, Jaspreet and Alia appeared for an interview for three vacancies in the same post. The probability of Rohit’s selection is `1/5`, Jaspreet’s selection is `1/3` and Alia’s selection is `1/4.` The event of selection is independent of each other.
|
Based on the above information, answer the following questions:
(i) What is the probability that at least one of them is selected? (1)
(ii) Find `P(G|barH)` where G is the event of Jaspreet’s selection and H denotes the event that Rohit is not selected. (1)
(iii) Find the probability that exactly one of them is selected. (2)
OR
(iii) Find the probability that exactly two of them are selected. (2)
Chapter:
|
A store has been selling calculators at ₹ 350 each. A market survey indicates that a reduction in price (p) of calculator increases the number of units (x) sold. The relation between the price and quantity sold is given by the demand function `p=450-1/2x.`
|
Based on the above information, answer the following questions:
- Determine the number of units (x) that should be sold to maximise the revenue R(x) = x p(x). Also, verify the result.
- What rebate in price of calculator should the store give to maximise the revenue?
Chapter:
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CBSE previous year question papers Class 12 Mathematics with solutions 2023 - 2024
Previous year Question paper for CBSE Class 12 Maths-2024 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CBSE Class 12.
How CBSE Class 12 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.