Question

Using integration, find the area bounded by the ellipse 9x² + 25y² = 225, the lines x = –2, x = 2, and the X-axis.

Answer 1

9x² + 25y² = 225

`x^2/25 + y^2/9 = 1`

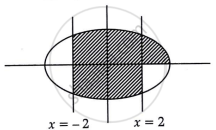
`A = int_-2^2 3/9 sqrt(25-x^2)`

`A = 6/9 int_-2^2 sqrt (25-x^2)`

`A = 6/9 [x/2 sqrt (25-x^2) + 25/2 sin^-1  x/5]_-2^2`

`A = 6/9 [x/2 sqrt (25-2^2) + 25/2 sin^-1  2/5]-[-2/2 sqrt (25-(-2)^2) + 25/2sin^-1  (-2)/5]`

`A = 6/9 [1xxsqrt21 + 25/2 sin^-1  2/5 + sqrt21 + 25/2 sin^-1  2/5]`

`A = 6/9 [2sqrt21 + 25 sin^-1  2/5]`

`A = 12/9 [sqrt21 + 25 sin^-1  2/5]`