Question

Find the distance between the line `x/2 = (2y-6)/4 = (1-z)/-1` and another line parallel to it passing through the point (4, 0, −5).

Answer 1

The given line cartesian form

`x/2 = (2y-6)/4 = (1-z)/-1`   ...(i)

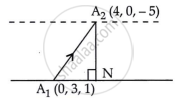
It passing through the point

A₁ with P.V. `veca_1 = 3hatj+hatk`

and it is parallel to the vector

`vecb = ahati+2hatj+hatk`

The equation of the line passing through the point A₂(4, 0, −5) with P.V.

`veca_2 = 4hati-5hatk` and parallel to the line (i) is

`vecr = 4hati-5hatk+μ(2hatj+hatk)`   ...(ii)

Now `veca_2-veca_1 = 4hati+0hatj-5hatk-0hati-3hatj-hatk`

`= 4hati-3hatj-6hatk`

`|vecb|= sqrt((0)^2+(2)^2+(1)^2)`

`=sqrt5`

and `vecbxx(veca_2-veca_1) = |(hati,hatj,hatk),(0,2,1),(4,-3,-6)|`

`=hati(-12-3)-hatj(0-4)+hatk(0-8)`

`=-15hati+4hatj-8hatk`

`|vecbxx(veca_2-veca_1)| = sqrt((-15)^2+(4)^2+(-8)^2)`

`= sqrt(225+16+64)`

`=sqrt305`

∴ The distance the parallel lines

(i) and (ii)

`= (vecbxx(veca_2-veca_1))/|vecb| = sqrt305/sqrt5`