Question

An iron ring of relative permeability µ_r has windings of insulated copper wire of n turns per meter. When the current in the windings is I, find the expression for the magnetic field in the ring.

Answer 1

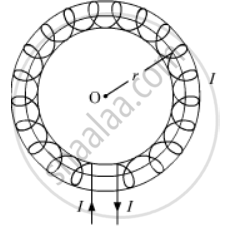
An iron ring of relative permeability µ_r having windings of insulated copper wire of n turns per meter can be considered as a toroid. Consider a toroidal solenoid with centre O as shown.

Suppose that
r = average radius of the toroid
I = current through the solenoid
To determine the magnetic field produced at the centre along the axis of the toroid due to current I, we imagine an Amperian loop of radius r and traverse it in the clockwise direction.
According to Ampere's circuital law, we have:

`ointvecB.vec(dl) = mu_rI`

The total current flowing through the toroid is NI, where N is the total number of turns.

`ointvecB.vec(dl) = mu_r(NI)` ......(1)

Now `vecB` and `vec(dl)` are in the same direction

`oint vecB.vec(dl) = B.ointdl`

`=> ointvecb.vec(dl) = B(2pir)` ....(2)

Comparing equations (1) and (2), we get:

`B(2pir) = mu_rNI`

`=> B = (mu_rNI)/(2pir)`

Now it is given that n is the number of turns per unit length, then

`n = N/(2pir)`

∴`B = mu_0nI` which is the expression for the magnetic field in the ring.