Advertisements
Advertisements
Question
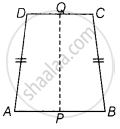
An isosceles trapezium has one line of symmetry.
Options
True
False
Solution
This statement is True.
Explanation:
Isosceles trapezium has only one line of symmetry along the line segment joining the mid-points of two parallel sides which is shown in figure.
APPEARS IN
RELATED QUESTIONS
Copy the figure with punched holes and find the axes of symmetry for the following:
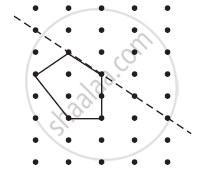
In the given figure, the mirror line (i.e., the line of symmetry) is given as a dotted line. Complete given figure performing reflection in the dotted (mirror) line. (You might perhaps place a mirror along the dotted line and look into the mirror for the image). Are you able to recall the name of the figure you complete?

The following figures have more than one line of symmetry. Such figures are said to have multiple lines of symmetry.
 |
 |
 |
| (a) | (b) | (c) |
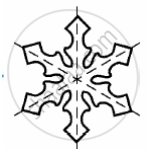
Identify multiple lines of symmetry, if any, in the following figure.
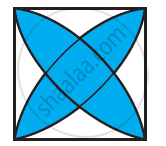
Copy the diagram and complete the given shape to be symmetric about the mirror line(s):
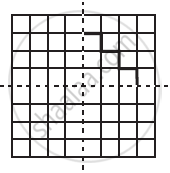
Copy the diagram and complete the given shape to be symmetric about the mirror line(s):
Find the line of symmetry and the order of rotational symmetry of the given regular polygons and complete the following table and answer the questions given below.
| Shape | Equilateral Triangle  |
Square |
Regular pentagon  |
Regular hexagon  |
Regular octagon  |
| Number of lines of symmetry | |||||
| Order of rotational symmetry |
i) A regular polygon of 10 sides will have _________ lines of symmetry
ii) If a regular polygon has 10 lines of symmetry, then its order of rotational symmetry is ___________
iii) A regular polygon of 'n' sides has _________ lines of symmetry and the order of rotational symmetry is _________
Draw the lines of symmetry in the following figure.
Look at the following shapes:
b) Which are the ones that will not look the same after the `1/3` turn? Mark them with (X).

A ______ triangle has no lines of symmetry.
By what minimum angle does a regular hexagon rotate so as to coincide with its original position for the first time?
