Advertisements
Chapters
2: Fractions and Decimals
3: Data Handling
4: Simple Equations
5: Lines and Angles
6: Triangles
7: Comparing Quantities
8: Rationals Numbers
9: Perimeter and Area
10: Algebraic Expressions
11: Exponents and Powers
▶ 12: Practical Geometry Symmetry and Visualising Solid Shapes
![NCERT Exemplar solutions for Mathematics [English] Class 7 chapter 12 - Practical Geometry Symmetry and Visualising Solid Shapes NCERT Exemplar solutions for Mathematics [English] Class 7 chapter 12 - Practical Geometry Symmetry and Visualising Solid Shapes - Shaalaa.com](/images/mathematics-english-class-7_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 12: Practical Geometry Symmetry and Visualising Solid Shapes
Below listed, you can find solutions for Chapter 12 of CBSE NCERT Exemplar for Mathematics [English] Class 7.
NCERT Exemplar solutions for Mathematics [English] Class 7 12 Practical Geometry Symmetry and Visualising Solid Shapes Exercise [Pages 364 - 383]
There are four options, out of which one is correct. Choose the correct one.
A triangle can be constructed by taking its sides as ______.
1.8 cm, 2.6 cm, 4.4 cm
2 cm, 3 cm, 4 cm
2.4 cm, 2.4 cm, 6.4 cm
3.2 cm, 2.3 cm, 5.5 cm
A triangle can be constructed by taking two of its angles as ______.
110°, 40°
70°, 115°
135°, 45°
90°, 90°
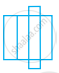
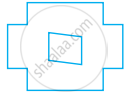
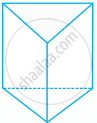
The number of lines of symmetry in the figure given below is ______.
4
8
6
Infinitely many
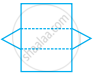
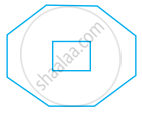
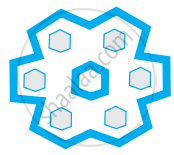
The number of lines of symmetry in the figure given below is ______.

1
3
6
Infinitely many
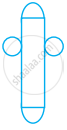
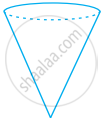
The order of rotational symmetry in the figure given below is ______.

4
8
6
Infinitely many
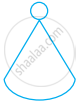
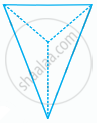
The order of rotational symmetry in the figure given below is ______.
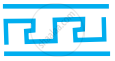
4
2
1
Infinitely many
The name of the given solid in the figure is ______.
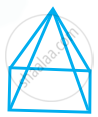
triangular pyramid
rectangular pyramid
rectangular prism
triangular prism
The name of the solid in figure is ______.
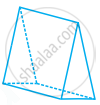
triangular pyramid
rectangular prism
triangular prism
rectangular pyramid
All faces of a pyramid are always ______.
Triangular
Rectangular
Congruent
None of these
A solid that has only one vertex is ______.
Pyramid
Cube
Cone
Cylinder
Out of the following which is a 3-D figure?
Square
Sphere
Triangle
Circle
Total number of edges a cylinder has ______.
0
1
2
3
A solid that has two opposite identical faces and other faces as parallelograms is a ______.
prism
pyramid
cone
sphere
The solid with one circular face, one curved surface and one vertex is known as ______.
cone
sphere
cylinder
prism
If three cubes each of edge 4 cm are placed end to end, then the dimensions of resulting solid are ______.
12 cm × 4 cm × 4 cm
4 cm × 8 cm × 4 cm
4 cm × 8 cm × 12 cm
4 cm × 6 cm × 8 cm
When we cut a corner of a cube as shown in the figure, we get the cutout piece a ______.
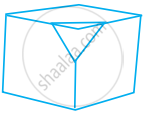
square pyramid
trapezium prism
triangular pyramid
a triangle
If we rotate a right-angled triangle of height 5 cm and base 3 cm about its height a full turn, we get ______.
cone of height 5 cm, base 3 cm
triangle of height 5 cm, base 3 cm
cone of height 5 cm, base 6 cm
triangle of height 5 cm, base 6 cm
If we rotate a right-angled triangle of height 5 cm and base 3 cm about its base, we get ______.
cone of height 3 cm and base 3 cm
cone of height 5 cm and base 5 cm
cone of height 5 cm and base 3 cm
cone of height 3 cm and base 5 cm
When a torch is pointed towards one of the vertical edges of a cube, you get a shadow of cube in the shape of ______.
square
rectangle but not a square
circle
triangle
Which of the following sets of triangles could be the lengths of the sides of a right-angled triangle?
3 cm, 4 cm, 6 cm
9 cm, 16 cm, 26 cm
1.5 cm, 3.6 cm, 3.9 cm
7 cm, 24 cm, 26 cm
In which of the following cases, a unique triangle can be drawn?
AB = 4 cm, BC = 8 cm and CA = 2 cm
BC = 5.2 cm, ∠B = 90° and ∠C = 110°
XY = 5 cm, ∠X = 45° and ∠Y = 60°
An isosceles triangle with the length of each equal side 6.2 cm
Which of the following has a line of symmetry?
Which of the following are reflections of each other?
Which of these nets is a net of a cube?
Which of the following nets is a net of a cylinder?
Which of the following letters of English alphabets have more than 2 lines of symmetry?
Take a square piece of paper as shown in figure (1). Fold it along its diagonals as shown in figure (2). Again fold it as shown in figure (3). Imagine that you have cut off 3 pieces of the form of congruent isosceles right-angled triangles out of it as shown in figure 4.
 |
 |
 |
 |
| (1) | (2) | (3) | (4) |
On opening the piece of paper which of the following shapes will you get?
Which of the following 3-dimensional figures has the top, side and front as triangles?
Fill in the blanks to make the statements true.
In an isosceles right triangle, the number of lines of symmetry is ______.
Rhombus is a figure that has ______ lines of symmetry and has a rotational symmetry of order ______.
______ triangle is a figure that has a line of symmetry but lacks rotational symmetry.
______ is a figure that has neither a line of symmetry nor a rotational symmetry.
______ and ______ are the capital letters of English alphabets that have one line of symmetry but they interchange to each other when rotated through 180°.
The common portion of two adjacent faces of a cuboid is called ______.
A plane surface of a solid enclosed by edges is called ______.
The corners of solid shapes are called its ______.
A solid with no vertex is ______.
A triangular prism has ______ faces, ______ edges and ______ vertices.
A triangular pyramid has ______ faces, ______ edges and ______ vertices.
A square pyramid has ______ faces, ______ edges and ______ vertices.
Out of ______ faces of a triangular prism, ______ are rectangles and ______ are triangles.
The base of a triangular pyramid is a ______.
Out of ______ faces of a square pyramid, ______ are triangles and ______ is/are squares.
Out of ______ faces of a rectangular pyramid ______ are triangles and base is ______.
Each of the letters H, N, S and Z has a rotational symmetry of order ______.
Order of rotational symmetry of a rectangle is ______.
Order of rotational symmetry of a circle is ______.
Each face of a cuboid is a ______.
Line of symmetry for an angle is its ______.
A parallelogram has ______ line of symmetry.
Order of rotational symmetry of  is ______.
is ______.
A ______ triangle has no lines of symmetry.
Cuboid is a rectangular ______.
A sphere has ______ vertex, ______ edge and ______ curved surface.
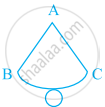 is a net of a ______ . `→` Circumference of circle = ______.
is a net of a ______ . `→` Circumference of circle = ______.
 is a net of a ______.
is a net of a ______.
Order of rotational symmetry of 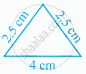 is ______.
is ______.
Identical cubes are stacked in the corner of a room as shown below. The number of cubes that are not visible are ______.
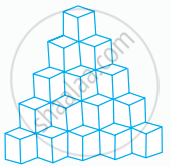
State whether the statements are True or False.
We can draw exactly one triangle whose angles are 70°, 30° and 80°.
True
False
The distance between the two parallel lines is the same everywhere.
True
False
A circle has two lines of symmetry.
True
False
An angle has two lines of symmetry.
True
False
A regular hexagon has six lines of symmetry.
True
False
An isosceles trapezium has one line of symmetry.
True
False
A parallelogram has two lines of symmetry.
True
False
Order of rotational symmetry of a rhombus is four.
True
False
An equilateral triangle has six lines of symmetry.
True
False
Order of rotational symmetry of a semi-circle is two.
True
False
In oblique sketch of the solid, the measurements are kept proportional.
True
False
An isometric sketch does not have proportional length.
True
False
A cylinder has no vertex.
True
False
All the faces, except the base of a square pyramid are triangular.
True
False
A pyramid has only one vertex.
True
False
A triangular prism has 5 faces, 9 edges and 6 vertices.
True
False
If the base of a pyramid is a square, it is called a square pyramid.
True
False
A rectangular pyramid has 5 rectangular faces.
True
False
Rectangular prism and cuboid refer to the same solid.
True
False
A tetrahedron has 3 triangular faces and 1 rectangular face.
True
False
While rectangle is a 2-D figure, cuboid is a 3-D figure.
True
False
While sphere is a 2-D figure, circle is a 3-D figure.
True
False
Two dimensional figures are also called plane figures.
True
False
A cone is a polyhedron.
True
False
A prism has four bases.
True
False
The number of lines of symmetry of a regular polygon is equal to the vertices of the polygon.
True
False
The order of rotational symmetry of a figure is 4 and the angle of rotation is 180° only.
True
False
After rotating a figure by 120° about its centre, the figure coincides with its original position. This will happen again if the figure is rotated at an angle of 240°.
True
False
Mirror reflection leads to symmetry always.
True
False
Rotation turns an object about a fixed point which is known as centre of rotation.
True
False
Isometric sheet divides the paper into small isosceles triangles made up of dots or lines.
True
False
The circle, the square, the rectangle and the triangle are examples of plane figures.
True
False
The solid shapes are of two-dimensional.
True
False
Triangle with length of sides as 5 cm, 6 cm and 11 cm can be constructed.
True
False
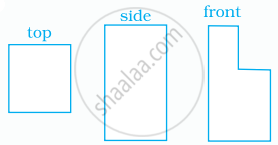
Draw the top, side and front views of the solids given below in the figure:

Draw the top, side and front views of the solids given below in the figure:
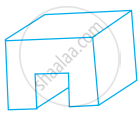
Draw a solid using the top. side and front views as shown below. [Use Isometric dot paper].
Construct a right-angled triangle whose hypotenuse measures 5 cm and one of the other sides measures 3.2 cm.
Construct a right-angled isosceles triangle with one side (other than hypotenuse) of length 4.5 cm.
Draw two parallel lines at a distance of 2.2 cm apart.
Draw an isosceles triangle with each of equal sides of length 3 cm and the angle between them as 45°.
Draw a triangle whose sides are of lengths 4 cm, 5 cm and 7 cm.
Construct an obtuse angled triangle which has a base of 5.5 cm and base angles of 30° and 120°.
Construct an equilateral triangle ABC of side 6 cm.
By what minimum angle does a regular hexagon rotate so as to coincide with its original position for the first time?
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry.

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry.

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry
[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the following figure, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
In the figure of a cube, Which edge is the intersection of faces EFGH and EFBA?

In the figure of a cube, Which faces intersect at edge FB?

In the figure of a cube, Which three faces form the vertex A?

In the figure of a cube, Which vertex is formed by the faces ABCD, ADHE and CDHG?

In the figure of a cube, Give all the edges that are parallel to edge AB.

In the figure of a cube, Give the edges that are neither parallel nor perpendicular to edge BC.

In the figure of a cube, Give all the edges that are perpendicular to edge AB.

In the figure of a cube, Give four vertices that do not all lie in one plane.

Draw a net of a cuboid having same breadth and height, but length double the breadth.
Draw the nets of the following:
Triangular prism
Draw the nets of the following:
Tetrahedron
Draw the nets of the following:
Cuboid
Draw a net of the solid given in the figure:
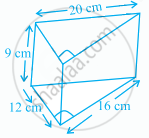
Draw an isometric view of a cuboid 6 cm × 4 cm × 2 cm.
The net given below in the figure can be used to make a cube. Which edge meets AN?
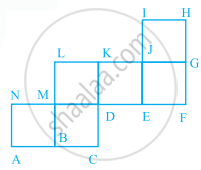
The net given below in the figure can be used to make a cube. Which edge meets DE?

Draw the net of triangular pyramid with base as equilateral triangle of side 3 cm and slant edges 5 cm.
Draw the net of a square pyramid with base as square of side 4 cm and slant edges 6 cm.
Draw the net of rectangular pyramid with slant edge 6 cm and base as rectangle with length 4 cm and breadth 3 cm.
Find the number of cubes in the following figure and give the top, front, left side and right side view (arrow indicating the front view).

Find the number of cubes in the following figure and give the top, front, left side and right side view (arrow indicating the front view).
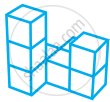
Find the number of cubes in the following figure and give the top, front, left side and right side view (arrow indicating the front view).

Find the number of cubes in the following figure and give the top, front, left side and right side view (arrow indicating the front view).

Find the number of cubes in the following figure and give the top, front, left side and right side view (arrow indicating the front view).

Find the number of cubes in the following figure and give the top, front, left side and right side view (arrow indicating the front view).
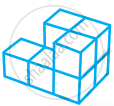
Find the number of cubes in the following figure and give the top, front, left side and right side view (arrow indicating the front view).

Find the number of cubes in the following figure and give the top, front, left side and right side view (arrow indicating the front view).
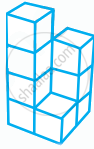
Draw all lines of symmetry for the following figure as given below:

Draw all lines of symmetry for the following figure as given below:

Draw all lines of symmetry for the following figure as given below:

How many faces does figure have?

Trace figure. Then draw all lines of symmetry, if it has.

Trace figure. Then draw all lines of symmetry, if it has.
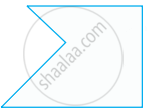
Trace figure. Then draw all lines of symmetry, if it has.
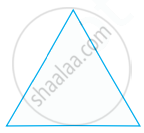
Tell whether the figure has rotational symmetry or not.

Yes
No
Tell whether the figure has rotational symmetry or not.

Yes
No
Tell whether the figure has rotational symmetry or not.

Yes
No
Tell whether the figure has rotational symmetry or not.

Yes
No
Tell whether the figure has rotational symmetry or not.
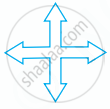
Yes
No
Tell whether the figure has rotational symmetry or not.

Yes
No
Draw all lines of symmetry for the following figure.

Draw all lines of symmetry for the following figure.

Draw all lines of symmetry for the following figure.

Draw all lines of symmetry for the following figure.

Draw all lines of symmetry for the following figure.

Draw all lines of symmetry for the following figure.
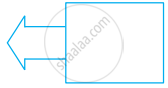
Tell whether the figure has rotational symmetry. Write yes or no.

Yes
No
Tell whether the figure has rotational symmetry. Write yes or no.

Yes
No
Tell whether the figure has rotational symmetry. Write yes or no.

Yes
No
Tell whether the figure has rotational symmetry. Write yes or no.

Yes
No
Does the figure have rotational symmetry?
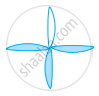
The flag of Japan is shown below. How many lines of symmetry does the flag have?

Which of the figure given below have both line and rotational symmetry?
| (a) | 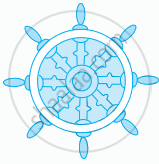 |
(b) | 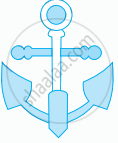 |
| (c) |  |
(d) |  |
Which of the following figure do not have line symmetry?
| (a) |  |
(b) |  |
| (c) |  |
(d) | 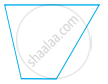 |
Which capital letters of English alphabet have no line of symmetry?
Solutions for 12: Practical Geometry Symmetry and Visualising Solid Shapes
![NCERT Exemplar solutions for Mathematics [English] Class 7 chapter 12 - Practical Geometry Symmetry and Visualising Solid Shapes NCERT Exemplar solutions for Mathematics [English] Class 7 chapter 12 - Practical Geometry Symmetry and Visualising Solid Shapes - Shaalaa.com](/images/mathematics-english-class-7_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
NCERT Exemplar solutions for Mathematics [English] Class 7 chapter 12 - Practical Geometry Symmetry and Visualising Solid Shapes
Shaalaa.com has the CBSE Mathematics Mathematics [English] Class 7 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. NCERT Exemplar solutions for Mathematics Mathematics [English] Class 7 CBSE 12 (Practical Geometry Symmetry and Visualising Solid Shapes) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. NCERT Exemplar textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 7 chapter 12 Practical Geometry Symmetry and Visualising Solid Shapes are Concept of Symmetry, Lines of Symmetry for Regular Polygons, Concept of Rotational Symmetry, Line Symmetry and Rotational Symmetry, Concept of Reflection Symmetry, Plane Figures and Solid Shapes, Nets for Building 3-d Shapes, Drawing Solids on a Flat Surface - Oblique Sketches, Drawing Solids on a Flat Surface - Isometric Sketches, Visualising Solid Objects, Viewing Different Sections of a Solid, Faces, Edges and Vertices, Construction of a Line Parallel to a Given Line, Through a Point Not on the Line, Construction of Triangles, Constructing a Triangle When the Length of Its Three Sides Are Known (SSS Criterion), Constructing a Triangle When the Lengths of Two Sides and the Measure of the Angle Between Them Are Known. (SAS Criterion), Constructing a Triangle When the Measures of Two of Its Angles and the Length of the Side Included Between Them is Given. (ASA Criterion), Constructing a Right-angled Triangle When the Length of One Leg and Its Hypotenuse Are Given (RHS Criterion).
Using NCERT Exemplar Mathematics [English] Class 7 solutions Practical Geometry Symmetry and Visualising Solid Shapes exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in NCERT Exemplar Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [English] Class 7 students prefer NCERT Exemplar Textbook Solutions to score more in exams.
Get the free view of Chapter 12, Practical Geometry Symmetry and Visualising Solid Shapes Mathematics [English] Class 7 additional questions for Mathematics Mathematics [English] Class 7 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.