Advertisements
Advertisements
Question
Answer the following :
ΔPQR is an equilateral triangle with side 18 cm. A circle is drawn on segment QR as diameter. Find the length of the arc of this circle within the triangle.
Solution
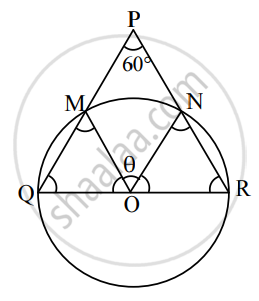
Let O be the centre of the circle drawn on QR as a diameter.
Let the circle intersect seg PQ and seg PR at points M and N respectively.
Since, `l("OQ") = l("OM")`,
∴ m∠OMQ = m∠OQM = 60°
∴ m∠MOQ = 60°
Similarly, m∠NOR = 60°
Given, QR = 18 cm
∴ r = 9 cm
∴ θ = 60°
= `(60 xx pi/180)^"c"`
= `pi^"c"/3`
∴ length of the arc MN = S = rθ
= `9 xx pi/3`
= 3π cm
APPEARS IN
RELATED QUESTIONS
Find the length of an arc of a circle which subtends an angle of 108° at the centre, if the radius of the circle is 15 cm.
The radius of a circle is 9 cm. Find the length of an arc of this circle which cuts off a chord of length, equal to length of radius.
Find the angle in degree subtended at the centre of a circle by an arc whose length is 15 cm, if the radius of the circle is 25 cm.
Two arcs of the same lengths subtend angles of 60° and 75° at the centres of two circles. What is the ratio of radii of two circles?
If two arcs of the same length in two circles subtend angles 65° and 110° at the centre. Find the ratio of their radii.
In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.
