Advertisements
Advertisements
Question
The radius of a circle is 9 cm. Find the length of an arc of this circle which cuts off a chord of length, equal to length of radius.
Solution
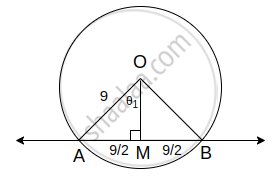
Here, r = 9 cm
Let AB be the chord of the circle with centre at O such that l(chord AB) = 9 cm. Let OM be the perpendicular drawn from the centre O to the chord AB.
Then M is the midpoint of AB.
∴ `l("AM") = 1/2 × l ("AB") = 9/2 = 1/2 × l ("OA")`
Let m∠AOM = θ1.
Then in right-angled triangle OMA,
sin θ1 = `"AM"/"OA" = ((9/2))/9 = 1/2`
∴ sin θ1 = sin 30°
∴ θ1 = 30°
∴ m∠AOB = θ = 2·m∠AOM= 2θ1
∴ θ = 60° = `(60 × π/180)^"c" = π^"c"/3`
∴ length of the arc = S = r·θ = 9 × `π/3` = 3π cm.
APPEARS IN
RELATED QUESTIONS
Find the length of an arc of a circle which subtends an angle of 108° at the centre, if the radius of the circle is 15 cm.
Find the angle in degree subtended at the centre of a circle by an arc whose length is 15 cm, if the radius of the circle is 25 cm.
Two arcs of the same lengths subtend angles of 60° and 75° at the centres of two circles. What is the ratio of radii of two circles?
Answer the following :
ΔPQR is an equilateral triangle with side 18 cm. A circle is drawn on segment QR as diameter. Find the length of the arc of this circle within the triangle.
If two arcs of the same length in two circles subtend angles 65° and 110° at the centre. Find the ratio of their radii.
In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.
