Question

Answer the following question.

A spherical surface separates two transparent media. Derive an expression that relates object and image distances with the radius of curvature for a point object. Clearly state the assumptions, if any.

Answer 1

1. Consider a spherical surface YPY′ of radius curvature R, separating two transparent media of refractive indices n₁ and n₂ respectively with n₁ < n₂.
2. P is the pole and X′PX is the principal axis. A point object O is at a distance u from the pole, in the medium of refractive index n₁.
3. In order to minimize spherical aberration, we consider two paraxial rays.
4. The ray OP along the principal axis travels undeviated along with PX. Another ray OA strikes the surface at A.
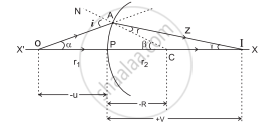
           Refraction at a single refracting surface
5. As n₁< n₂, the ray deviates towards the normal (CAN), travels along with AZ, and a real image of point object O is formed at I.
6. Let α, β and ϒ be the angles subtended by incident ray, normal and refracted ray with the principal axis.
   ∴ i = (α + β) and r = (β − γ)
7. As the rays are paraxial, all the angles can be considered to be very small.,
   i.e., sin i ≈ i and sin r ≈ r
   Angles α, β, and ϒ can also be expressed as,
   α = `"arcPA"/"OP"="arcPA"/-"u"`,
   β = `"arcPA"/"PC"="arcPA"/"R"`
   and γ = `"arcPA"/"PI"="arcPA"/"v"`
8. According to Snell’s law,
   n₁ sin (i) = n₂ sin (r)
   For small angles, Snell’s law can be written as, n₁i = n₂r
   ∴ n₁ (α + β) = n₂ (β − ϒ)
   (n₂ − n₁) β = n₁α + n₂γ
   Substituting values of α, β and ϒ, we get,
   (n₂ − n₁) `"arcPA"/"R"="n"_1("arcPA"/-"u")+"n"_2("arcPA"/"v")`
   ∴ `("n"_2-"n"_1)/"R"="n"_2/"v"-"n"_1/"u"`

Assumptions:

To derive an expression that relates object and image distances with the radius of curvature for a point object, the two rays considered are assumed to be paraxial thus making the angles subtended by incident ray, normal and refracted ray with the principal axis very small.