Advertisements
Advertisements
Question
As shown in the figure, a cylindrical glass contains water. A metal sphere of diameter 2 cm is immersed in it. Find the volume of the water.

Solution
Radius of the metallic sphere, r = \[\frac{2}{2}\] 1 cm
Radius of the cylindrical glass, R = \[\frac{14}{2}\] = 7 cm
Height of water in cylindrical glass, H = 30 cm
∴ Volume of the water = Volume of water in the cylindrical glass − Volume of the metallic sphere
\[= \pi R^2 H - \frac{4}{3}\pi r^3 \]
\[ = \pi \left( 7 \right)^2 \times 30 - \frac{4}{3}\pi \times \left( 1 \right)^3 \]
\[ = 1470\pi - 1 . 33\pi\]
\[ = 1468 . 67\pi {cm}^3\]
Thus, the volume of the water is 1468.67π cm3 .
APPEARS IN
RELATED QUESTIONS
Find the surface area of a sphere of radius 4.2 cm. (π = `22/7`)
Find the diagonal of a square whose side is 10 cm.
The volume of a cube is 1000 cm3. Find the side of a cube.
The volume of a cube is 512 cm3. Find its side.
The radius and slant height of a cone are 5 cm and 20 cm respectively. Find its curved surface area. (Π = 3.14)
If ‘V’ is the volume of a cuboid of dimensions a × b × c and ‘S’ is its surface area, then prove that: `1/V = 2/S[1/a +1/b + 1/c]`
The dimensions of a cuboid in cm are 50 × 18 × 10. Find its volume.
The volume of a cube is 343 cm3. Find its total surface area.
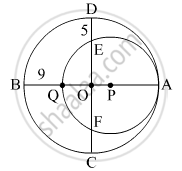
In the given figure, two circles with centres O and P are touching internally at point A. If BQ = 9, DE = 5, complete the following activity to find the radii of the circles.
Find the volume and surface area of a sphere of radius 8.4 cm.
`(pi=22/7)`
The dimensions of a cuboid in cm are 30 × 18 × 10. Find its volume.
The volume of a cube is 1000 cm3. Find its total surface area.
Find the volume of a cube with side 6 cm.
The length, breadth, and height of a cuboid are in the ratio 5:4: 2. If the total surface area is 1216 cm2, find dimensions of the solid.
Find the volume of a cube of side 3 cm ______.
Water is flowing at the rate of 15 km/h through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in pond rise by 21 cm?
What should be the speed of water if the rise in water level is to be attained in 1 hour?
