Advertisements
Advertisements
Question
Solution
Radius of the sphere, R = 9 cm
Radius of the wire, r = \[\frac{4}{2}\] = 2 mm = \[\frac{2}{10}\] = 0.2 cm ...[∵ 1 cm = 10 mm]
Let the length of the wire be l cm.
It is given that the metallic sphere is melted to make the wire.
∴ Volume of metal in the wire = Volume of the metallic sphere
\[\Rightarrow \pi r^2 l = \frac{4}{3}\pi R^3 \]
\[ \Rightarrow l = \frac{\frac{4}{3} R^3}{r^2}\]
\[ \Rightarrow l = \frac{\frac{4}{3} \times \left( 9 \right)^3}{\left( 0 . 2 \right)^2}\]
\[ \Rightarrow l = 24300 \text{ cm } \]
\[\Rightarrow l = \frac{24300}{100}\]
l = 243 m ...[∵ 1 m = 100 cm]
Thus, the length of the wire is 243 m.
APPEARS IN
RELATED QUESTIONS
Find the surface area of a sphere of radius 4.2 cm. (π = `22/7`)
The volume of a cube is 1000 cm3. Find the side of a cube.
Find the volume and surface area of a sphere of radius 2.1 cm. `(pi=22/7)`
The sum of length, breadth and height of a cuboid is 38 cm and the length of its diagonal is 22 cm. Find the total surface area of the cuboid.
The volume of a cube is 512 cm3. Find its side.
The radius and slant height of a cone are 5 cm and 20 cm respectively. Find its curved surface area. (Π = 3.14)
If ‘V’ is the volume of a cuboid of dimensions a × b × c and ‘S’ is its surface area, then prove that: `1/V = 2/S[1/a +1/b + 1/c]`
The volume of a cube is 343 cm3. Find its total surface area.
As shown in the figure, a cylindrical glass contains water. A metal sphere of diameter 2 cm is immersed in it. Find the volume of the water.

The diameter and thickness of a hollow metals sphere are 12 cm and 0.01 m respectively. The density of the metal is 8.88 gm per cm3. Find the outer surface area and mass of the sphere.
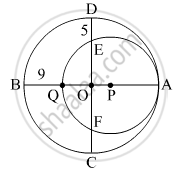
In the given figure, two circles with centres O and P are touching internally at point A. If BQ = 9, DE = 5, complete the following activity to find the radii of the circles.
Select the correct alternative answer and write it.
What is the total surface area of a solid hemisphere whose radius is r ?
The dimensions of a cuboid in cm are 30 × 18 × 10. Find its volume.
The volume of a cube is 1000 cm3. Find its total surface area.
Find the volume of a cube with side 6 cm.
The length, breadth, and height of a cuboid are in the ratio 5:4: 2. If the total surface area is 1216 cm2, find dimensions of the solid.
Water is flowing at the rate of 15 km/h through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in pond rise by 21 cm?
What should be the speed of water if the rise in water level is to be attained in 1 hour?
A cylinder of radius 12 cm contains water up to the height 20 cm. A spherical iron ball is dropped into the cylinder and thus water level raised by 6.75 cm. What is the radius of iron ball?
