Advertisements
Advertisements
Question
Assuming that the length of the solenoid is large when compared to its diameter, find the equation for its inductance.
Advertisements
Solution
Consider a long solenoid of length l and cross-sectional area A. Let n be the number of turns per unit length (or turn density) of the solenoid. When an electric current i is passed through the solenoid, a magnetic field is produced by it which is almost uniform and is directed along the axis of the solenoid. The magnetic field at any point inside the solenoid is given by
B = μ0ni
As this magnetic field passes through the solenoid, the windings of the solenoid are linked by the field lines. The magnetic flux passing through each turn is
`Φ_"B" = int_"A" vec"B"*"d"vec"A" = "BA" cos theta = "BA"` ..(since θ = 0°)
`Φ_"B" = (mu_0 "ni")"A"`
The total magnetic flux linked or flux linkage of the solenoid with N turns (the total number of turns N is given by N = nl) is
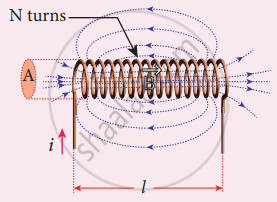
Self-inductance of a long solenoid
NΦB = n (nl) (μ0ni)A
NΦB = (μ0n2Al)i ….. (1)
From the self-induction
NΦB = LI ….. (2)
Comparing equations (1) and (2), we have L = μ0n2Al
From the above equation, it is clear that inductance depends on the geometry of the solenoid (turn density n, cross-sectional area A, length l) and the medium present inside the solenoid. If the solenoid is filled with a dielectric medium of relative permeability μr, then
L = μ0
L = μn0μrn2Al
APPEARS IN
RELATED QUESTIONS
When the current changes from +2A to −2A in 0.05 s, an emf of 8 V is induced in a coil. The co-efficient of self-induction of the coil is
A circular coil with a cross-sectional area of 4 cm2 has 10 turns. It is placed at the centre of a long solenoid that has 15 turns/cm and a cross-sectional area of 10 cm2. The axis of the coil coincides with the axis of the solenoid. What is their mutual inductance?
What do you mean by self-induction?
Define self-inductance of a coil interms of
- magnetic flux and
- induced emf
How will you define the unit of inductance?
What do you understand by self-inductance of a coil?
An inductor of inductance L carries an electric current i. How much energy is stored while establishing the current in it?
Two air core solenoids have the same length of 80 cm and same cross–sectional area 5 cm2. Find the mutual inductance between them if the number of turns in the first coil is 1200 turns and that in the second coil is 400 turns.
A long solenoid having 400 turns per cm carries a current 2A. A 100 turn coil of cross-sectional area 4 cm2 is placed co-axially inside the solenoid so that the coil is in the field produced by the solenoid. Find the emf induced in the coil if the current through the solenoid reverses its direction in 0.04 sec.
The solenoids S1 and S2 are wound on an iron-core of relative permeability 900. The area of their cross-section and their length are the same and are 4 cm2 and 0.04 m, respectively. If the number of turns in S1 is 200 and that in S2 is 800, calculate the mutual inductance between the coils. The current in solenoid 1 is increased from 2A to 8A in 0.04 second. Calculate the induced emf in solenoid 2.
