Advertisements
Advertisements
Question
बाजूंच्या लांबी a, b, c असलेल्या त्रिकोणामध्ये जर a2 + b2 = c2 असेल तर तो कोणत्या प्रकारचा त्रिकोण असेल?
Options
विशालकोन त्रिकोण
लघुकोन त्रिकोण
काटकोन त्रिकोण
समभुज त्रिकोण
Solution
बाजूंच्या लांबी a, b, c असलेल्या त्रिकोणामध्ये जर a2 + b2 = c2 असेल तर तो काटकोन त्रिकोण असेल.
RELATED QUESTIONS
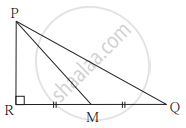
आकृती मध्ये M हा बाजू QR चा मध्यबिंदू आहे. ∠PRQ = 90° असेल तर सिद्ध करा, PQ2 = 4PM2 - 3PR2
रस्त्याच्या दुतर्फा असलेल्या इमारतीच्या भिंती एकमेकींना समांतर आहेत. 5.8 मी लांबीच्या शिडीचे एक टोक रस्त्यावर ठेवले असता तिचे वरचे टोक पहिल्या इमारतीच्या 4 मीटर उंच असलेल्या खिडकीपर्यंत टेकते. त्याच ठिकाणी शिडी ठेवून रस्त्याच्या दुसऱ्या बाजूस वळविल्यास तिचे वरचे टोक दुसऱ्या इमारतीच्या 4.2 मीटर उंच असलेल्या खिडकीपर्यंत येते, तर रस्त्याची रुंदी काढा.
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
काटकोन त्रिकोणात काटकोन करणाऱ्या बाजूंच्या वर्गांची बेरीज 169 असेल, तर त्याच्या कर्णाची लांबी किती?
काटकोन त्रिकोणामध्ये काटकोन करणाऱ्या बाजू 24 सेमी व 18 सेमी असतील तर त्याच्या कर्णाची लांबी ______ असेल.
आयताचे क्षेत्रफळ 192 चौसेमी असून त्याची लांबी 16 सेमी आहे, तर आयताच्या कर्णाची लांबी काढा.
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका आयताची एक बाजू 12 आणि कर्णाची लांबी 20 असेल, तर त्या आयताच्या दुसऱ्या बाजूची लांबी किती?
एका आयताच्या बाजू अनुक्रमे 35 मीटर आणि 12 मीटर असल्यास त्याचा कर्ण किती?
सोबतच्या आकृतीत, ∆ABC मध्ये, AD ⊥ BC, तर AB2 + CD2 = BD2 + AC2 हे सिद्ध करण्यासाठी खालील कृती पूर्ण करा.
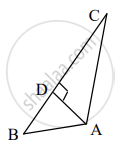
कृती: पायथागोरसच्या प्रमेयानुसार, काटकोन त्रिकोण ∆ADC मध्ये,
AC2 = AD2 + `square^2`
∴ AD2 = AC2 – CD2 …...........(i)
तसेच, पायथागोरसच्या प्रमेयानुसार, काटकोन त्रिकोण ∆ABD मध्ये,
AB2 = `square^2` + BD2
∴ AD2 = AB2 – BD2 …...… (ii)
∴ `square^2 - "BD"^2 = "AC"^2 - square^2` .....…….. (i) व (ii) वरून
∴ AB2 + CD2 = AC2 + BD2
सोबतच्या आकृतीत, ∆QPR मध्ये, ∠QPR = 90°, PM ⊥ QR, PM = 10, QM = 8 यावरून QR काढण्यासाठी खालील कृती पूर्ण करा.
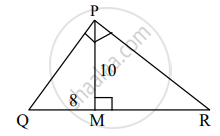
कृती:
∆PQR मध्ये, PM ⊥ QR
∠PMQ = 90°,
∆PMQ मध्ये, पायथागोरसच्या प्रमेयानुसार,
PM2 + `square` = PQ2 …(i)
∴ PQ2 = 102 + 82
∴ PQ2 = `square` + 64
PQ = `sqrt164`
∠PMR = 90°
यावरून, ∆QPR ~ ∆QMP ~ ∆PMR
∴ ∆QMP ~ ∆PMR
∴ `"PM"/"RM" = "QM"/"PM"`
∴ PM2 = RM × QM
∴ 102 = RM × 8
RM = `100/8 = square` आणि QR = QM + MR
QR = `square + 25/2 = 41/2`
एका आयताचे क्षेत्रफळ 192 चौसेमी असून त्याची लांबी 16 सेमी आहे, तर त्या आयताच्या कर्णाची लांबी माहीत करण्यासाठी कृती पूर्ण करा.
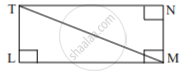
कृती: सोबतच्या आकृतीत, `square`LMNT हा आयत आहे.
आयताचे क्षेत्रफळ = लांबी × रुंदी
∴ आयताचे क्षेत्रफळ = `square` × रुंदी
रुंदी = 12 सेमी
∠TLM = 90° [आयताचा प्रत्येक कोन काटकोन असतो.]
∆TLM मध्ये, पायथागोरसच्या प्रमेयानुसार,
TL2 + `square` = TM2
TM2 = `square` + 122
TM2 = `square` + 144
TM = 20
