Advertisements
Advertisements
Question
सोबतच्या आकृतीत, ∆QPR मध्ये, ∠QPR = 90°, PM ⊥ QR, PM = 10, QM = 8 यावरून QR काढण्यासाठी खालील कृती पूर्ण करा.
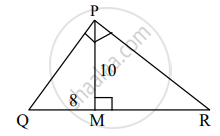
कृती:
∆PQR मध्ये, PM ⊥ QR
∠PMQ = 90°,
∆PMQ मध्ये, पायथागोरसच्या प्रमेयानुसार,
PM2 + `square` = PQ2 …(i)
∴ PQ2 = 102 + 82
∴ PQ2 = `square` + 64
PQ = `sqrt164`
∠PMR = 90°
यावरून, ∆QPR ~ ∆QMP ~ ∆PMR
∴ ∆QMP ~ ∆PMR
∴ `"PM"/"RM" = "QM"/"PM"`
∴ PM2 = RM × QM
∴ 102 = RM × 8
RM = `100/8 = square` आणि QR = QM + MR
QR = `square + 25/2 = 41/2`
Advertisements
Solution
∆PQR मध्ये, PM ⊥ QR
∠PMQ = 90°,
∆∆PMQ मध्ये, पायथागोरसच्या प्रमेयानुसार,
PM2 + QM2 = PQ2 …(i)
∴ PQ2 = 102 + 82
∴ PQ2 = 100 + 64
= 164
PQ = `sqrt164`
∠PMR = 90°
यावरून, ∆QPR ~ ∆QMP ~ ∆PMR
∴ ∆QMP ~ ∆PMR
∴ `"PM"/"RM" = "QM"/"PM"` ...................[समरूप त्रिकोणांच्या संगत बाजू]
∴ PM2 = RM × QM
∴ 102 = RM × 8
RM = `100/8 = underline(25/2)`
आणि QR = QM + MR
QR = `underline(8) + 25/2 = 41/2`
APPEARS IN
RELATED QUESTIONS
प्रणाली आणि प्रसाद एकाच ठिकाणावरून पूर्व आणि उत्तर दिशेला सारख्या वेगाने निघाले. दोन तासांनंतर त्यांच्यामधील अंतर `15sqrt2` किमी असेल तर त्यांचा ताशी वेग काढा.
ΔABC मध्ये ∠BAC = 90°, रेख BL व रेख CM या ΔABC च्या मध्यगा आहेत, तर सिद्ध करा : 4(BL2 + CM2 ) = 5BC2.
समलंब चौकोन ABCD मध्ये, रेख AB || रेख DC रेख BD ⊥ रेख AD, रेख AC ⊥ रेख BC, जर AD = 15, BC = 15 आणि AB = 25 असेल तर A(`square`ABCD) किती?
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका चौरसाच्या कर्णाची लांबी `sqrt2` सेमी असेल, तर त्या चौरसाच्या प्रत्येक बाजूची लांबी किती?
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका आयताची एक बाजू 12 आणि कर्णाची लांबी 20 असेल, तर त्या आयताच्या दुसऱ्या बाजूची लांबी किती?
एका आयताच्या बाजू अनुक्रमे 35 मीटर आणि 12 मीटर असल्यास त्याचा कर्ण किती?
सोबतच्या आकृतीत, ∆ABC मध्ये, AD ⊥ BC, तर AB2 + CD2 = BD2 + AC2 हे सिद्ध करण्यासाठी खालील कृती पूर्ण करा.
कृती: पायथागोरसच्या प्रमेयानुसार, काटकोन त्रिकोण ∆ADC मध्ये,
AC2 = AD2 + `square^2`
∴ AD2 = AC2 – CD2 …...........(i)
तसेच, पायथागोरसच्या प्रमेयानुसार, काटकोन त्रिकोण ∆ABD मध्ये,
AB2 = `square^2` + BD2
∴ AD2 = AB2 – BD2 …...… (ii)
∴ `square^2 - "BD"^2 = "AC"^2 - square^2` .....…….. (i) व (ii) वरून
∴ AB2 + CD2 = AC2 + BD2
काटकोन त्रिकोणात काटकोन करणाऱ्या बाजू 9 सेमी व 12 सेमी आहेत, तर त्या त्रिकोणाच्या कर्णाची लांबी माहीत करण्यासाठी कृती पूर्ण करा.
कृती: ∆PQR मध्ये, ∠PQR = 90°
पायथागोरसच्या प्रमेयानुसार,
PQ2 + `square` = PR2 .........…(i)
PR2 = 92 + 122
PR2 = `square + 144`
∴ PR2 = `square`
∴ PR = 15
त्रिकोणाचा कर्ण = `square`
सोबतच्या आकृतीत, ∠DFE = 90°, FG ⊥ ED, जर GD = 8, FG = 12, lej (1) EG, (2) FD आणि (3) EF काढा.
वरील आकृतीत `square`ABCD हा आयत आहे. जर AB = 5, AC = 13, तर बाजू BC ची लांबी काढण्यासाठी खालील कृती पर्ण करा.
कृती: ΔABC हा `square` त्रिकोण आहे.
∴ पायथागोरसच्या प्रमेयानुसार,
AB2 + BC2 = AC2
∴ 25 + BC2 = `square`
∴ BC2 = `square`
∴ BC = `square`
