Advertisements
Advertisements
प्रश्न
सोबतच्या आकृतीत, ∆QPR मध्ये, ∠QPR = 90°, PM ⊥ QR, PM = 10, QM = 8 यावरून QR काढण्यासाठी खालील कृती पूर्ण करा.
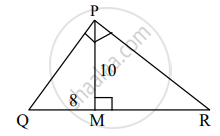
कृती:
∆PQR मध्ये, PM ⊥ QR
∠PMQ = 90°,
∆PMQ मध्ये, पायथागोरसच्या प्रमेयानुसार,
PM2 + `square` = PQ2 …(i)
∴ PQ2 = 102 + 82
∴ PQ2 = `square` + 64
PQ = `sqrt164`
∠PMR = 90°
यावरून, ∆QPR ~ ∆QMP ~ ∆PMR
∴ ∆QMP ~ ∆PMR
∴ `"PM"/"RM" = "QM"/"PM"`
∴ PM2 = RM × QM
∴ 102 = RM × 8
RM = `100/8 = square` आणि QR = QM + MR
QR = `square + 25/2 = 41/2`
उत्तर
∆PQR मध्ये, PM ⊥ QR
∠PMQ = 90°,
∆∆PMQ मध्ये, पायथागोरसच्या प्रमेयानुसार,
PM2 + QM2 = PQ2 …(i)
∴ PQ2 = 102 + 82
∴ PQ2 = 100 + 64
= 164
PQ = `sqrt164`
∠PMR = 90°
यावरून, ∆QPR ~ ∆QMP ~ ∆PMR
∴ ∆QMP ~ ∆PMR
∴ `"PM"/"RM" = "QM"/"PM"` ...................[समरूप त्रिकोणांच्या संगत बाजू]
∴ PM2 = RM × QM
∴ 102 = RM × 8
RM = `100/8 = underline(25/2)`
आणि QR = QM + MR
QR = `underline(8) + 25/2 = 41/2`
APPEARS IN
संबंधित प्रश्न
एका आयताची लांबी 35 सेमी व रुंदी 12 सेमी आहे तर त्या आयताच्या कर्णाची लांबी काढा.
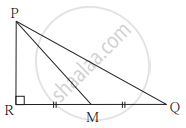
आकृती मध्ये M हा बाजू QR चा मध्यबिंदू आहे. ∠PRQ = 90° असेल तर सिद्ध करा, PQ2 = 4PM2 - 3PR2
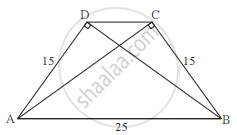
समलंब चौकोन ABCD मध्ये, रेख AB || रेख DC रेख BD ⊥ रेख AD, रेख AC ⊥ रेख BC, जर AD = 15, BC = 15 आणि AB = 25 असेल तर A(`square`ABCD) किती?
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका आयताची एक बाजू 12 आणि कर्णाची लांबी 20 असेल, तर त्या आयताच्या दुसऱ्या बाजूची लांबी किती?
एका काटकोन त्रिकोणामध्ये काटकोन करणाऱ्या बाजू 24 सेमी व 18 सेमी असतील, तर त्याच्या कर्णाची लांबी काढा.
एका आयताच्या बाजू अनुक्रमे 35 मीटर आणि 12 मीटर असल्यास त्याचा कर्ण किती?
सोबतच्या आकृतीत, ∆ABC मध्ये, AD ⊥ BC, तर AB2 + CD2 = BD2 + AC2 हे सिद्ध करण्यासाठी खालील कृती पूर्ण करा.
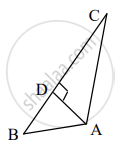
कृती: पायथागोरसच्या प्रमेयानुसार, काटकोन त्रिकोण ∆ADC मध्ये,
AC2 = AD2 + `square^2`
∴ AD2 = AC2 – CD2 …...........(i)
तसेच, पायथागोरसच्या प्रमेयानुसार, काटकोन त्रिकोण ∆ABD मध्ये,
AB2 = `square^2` + BD2
∴ AD2 = AB2 – BD2 …...… (ii)
∴ `square^2 - "BD"^2 = "AC"^2 - square^2` .....…….. (i) व (ii) वरून
∴ AB2 + CD2 = AC2 + BD2
10 मीटर लांबीची एक शिडी जमिनीपासून 8 मीटर उंचीच्या एका खिडकीपाशी पोहोचते, तर त्या भिंतीचा पाया व शिडीचे खालचे टोक यांमधील अंतर काढण्यासाठी खालील कृती पूर्ण करा.
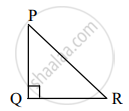
कृती: समजा, सोबतच्या आकृतीत,
PQ ही भिंतीची उंची आहे.
PR ही शिडी आहे आणि QR त्या भिंतीचा पाया व शिडीचे खालचे टोक यांमधील अंतर आहे.
∆PQR मध्ये, ∠PQR = 90°,
पायथागोरसच्या प्रमेयानुसार, PQ2 + `square` = PR2 … (i)
PR = 10, PQ = `square`
या किमती (i) मध्ये ठेवून,
QR2 + 82 = 102
QR2 = 102 – 82
QR2 = `square - 64`
QR2 = `square`
QR = 6
यावरून, त्या भिंतीचा पाया व शिडीचे खालचे टोक यांमधील अंतर 6 मीटर आहे.
∆LMN मध्ये, l = 5, m = 13, n = 12, तर ∆LMN हा काटकोन त्रिकोण आहे किंवा नाही ते ठरवण्यासाठी कृती करा. [l, m, n या ∠L, ∠M, व ∠N यांच्या समोरील बाजू आहेत.]
कृती: ∆LMN मध्ये, l = 5, m = 13, n = `square`
l2 = `square`, m2 = 169; n2 = 144.
l2 + n2 = 25 + 144 = `square`
`square^2` + l2 = m2
∴ पायथागोरसच्या प्रमेयानुसार, ∆LMN हा काटकोन त्रिकोण आहे.
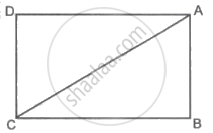
वरील आकृतीत `square`ABCD हा आयत आहे. जर AB = 5, AC = 13, तर बाजू BC ची लांबी काढण्यासाठी खालील कृती पर्ण करा.
कृती: ΔABC हा `square` त्रिकोण आहे.
∴ पायथागोरसच्या प्रमेयानुसार,
AB2 + BC2 = AC2
∴ 25 + BC2 = `square`
∴ BC2 = `square`
∴ BC = `square`
