Advertisements
Advertisements
Question
एका काटकोन त्रिकोणामध्ये कर्णाची लांबी 25 सेमी व उंची 7 सेमी असेल, तर त्याच्या पायाची लांबी काढा.
Solution
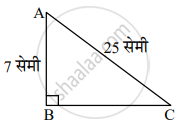
समजा, ∆ABC हा काटकोन त्रिकोण आहे.
AC = 25 सेमी, AB = 7 सेमी
∆ABC मध्ये, ∠B = 90° .....…[पक्ष]
∴ AC2 = AB2 + BC2 ….....[पायथागोरसचे प्रमेय]
∴ 252 = 72 + BC2
∴ 625 = 49 + BC2
∴ BC2 = 625 – 49
∴ BC2 = 576
∴ BC = 24 सेमी ….....[दोन्ही बाजूंचे वर्गमूळ घेऊन]
∴ काटकोन त्रिकोणाच्या पायाची लांबी 24 सेमी आहे.
APPEARS IN
RELATED QUESTIONS
एका चौरसाचा कर्ण 10 सेमी आहे तर त्याच्या बाजूची लांबी व परिमिती काढा.
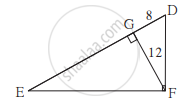
आकृती मध्ये ∠DFE = 90°, रेख FG ⊥ रेख ED. जर GD = 8, FG = 12, तर (1) EG (2) FD आणि (3) EF काढा.
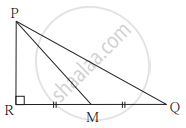
आकृती मध्ये M हा बाजू QR चा मध्यबिंदू आहे. ∠PRQ = 90° असेल तर सिद्ध करा, PQ2 = 4PM2 - 3PR2
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
काटकोन त्रिकोणात काटकोन करणाऱ्या बाजूंच्या वर्गांची बेरीज 169 असेल, तर त्याच्या कर्णाची लांबी किती?
आयताच्या बाजू 11 सेमी व 60 सेमी असतील, तर त्याच्या कर्णाची लांबी काढा.
आयताचे क्षेत्रफळ 192 चौसेमी असून त्याची लांबी 16 सेमी आहे, तर आयताच्या कर्णाची लांबी काढा.
ΔABC मध्ये रेख AD ⊥ रेख BC आणि DB = 3CD, तर सिद्ध करा : 2AB2 = 2AC2 + BC2
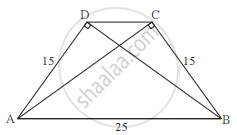
समलंब चौकोन ABCD मध्ये, रेख AB || रेख DC रेख BD ⊥ रेख AD, रेख AC ⊥ रेख BC, जर AD = 15, BC = 15 आणि AB = 25 असेल तर A(`square`ABCD) किती?
∆LMN मध्ये, l = 5, m = 13, n = 12, तर ∆LMN हा काटकोन त्रिकोण आहे किंवा नाही ते ठरवण्यासाठी कृती करा. [l, m, n या ∠L, ∠M, व ∠N यांच्या समोरील बाजू आहेत.]
कृती: ∆LMN मध्ये, l = 5, m = 13, n = `square`
l2 = `square`, m2 = 169; n2 = 144.
l2 + n2 = 25 + 144 = `square`
`square^2` + l2 = m2
∴ पायथागोरसच्या प्रमेयानुसार, ∆LMN हा काटकोन त्रिकोण आहे.
सोबतच्या आकृतीत, ∠DFE = 90°, FG ⊥ ED, जर GD = 8, FG = 12, lej (1) EG, (2) FD आणि (3) EF काढा.