Advertisements
Advertisements
Question
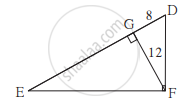
आकृती मध्ये ∠DFE = 90°, रेख FG ⊥ रेख ED. जर GD = 8, FG = 12, तर (1) EG (2) FD आणि (3) EF काढा.
Solution
(1) ΔDEF मध्ये, ∠DFE = 90° आणि रेख FG ⊥ रेख ED .....[पक्ष]
∴ FG2 = GD × EG ....[भूमितीमध्याचे प्रमेय]
∴ 122 = 8 × EG
∴ EG = `144/8`
∴ EG = 18 एकक
(2) ΔFGD मध्ये, ∠FGD = 90° .....[पक्ष]
∴ FD2 = FG2 + GD2 ....[पायथागोरसचे प्रमेय]
= 122 + 82
= 144 + 64
= 208
∴ FD = `sqrt(208)` .....[दोन्ही बाजूंचे वर्गमूळ घेऊन]
∴ FD = `4sqrt(13)` एकक
(3) ΔEGF मध्ये, ∠EGF = 90° .....[पक्ष]
∴ EF2 = EG2 + FG2 ....[पायथागोरसचे प्रमेय]
= 182 + 122
= 324 + 144
= 468
∴ EF = `sqrt(468)` .....[दोन्ही बाजूंचे वर्गमूळ घेऊन]
∴ EF = `6sqrt(13)` एकक
APPEARS IN
RELATED QUESTIONS
एका आयताची लांबी 35 सेमी व रुंदी 12 सेमी आहे तर त्या आयताच्या कर्णाची लांबी काढा.
आयताचे क्षेत्रफळ 192 चौसेमी असून त्याची लांबी 16 सेमी आहे, तर आयताच्या कर्णाची लांबी काढा.
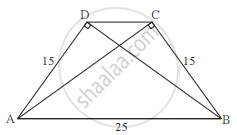
समलंब चौकोन ABCD मध्ये, रेख AB || रेख DC रेख BD ⊥ रेख AD, रेख AC ⊥ रेख BC, जर AD = 15, BC = 15 आणि AB = 25 असेल तर A(`square`ABCD) किती?
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका आयताची एक बाजू 12 आणि कर्णाची लांबी 20 असेल, तर त्या आयताच्या दुसऱ्या बाजूची लांबी किती?
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका समभुज चौकोनाच्या कर्णाची लांबी अनुक्रमे 60 व 80 असेल, तर त्या समभुज चौकोनाच्या बाजूची लांबी किती?
10 मीटर लांबीची एक शिडी जमिनीपासून 8 मीटर उंचीच्या एका खिडकीपाशी पोहोचते, तर त्या भिंतीचा पाया व शिडीचे खालचे टोक यांमधील अंतर काढण्यासाठी खालील कृती पूर्ण करा.
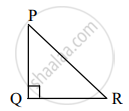
कृती: समजा, सोबतच्या आकृतीत,
PQ ही भिंतीची उंची आहे.
PR ही शिडी आहे आणि QR त्या भिंतीचा पाया व शिडीचे खालचे टोक यांमधील अंतर आहे.
∆PQR मध्ये, ∠PQR = 90°,
पायथागोरसच्या प्रमेयानुसार, PQ2 + `square` = PR2 … (i)
PR = 10, PQ = `square`
या किमती (i) मध्ये ठेवून,
QR2 + 82 = 102
QR2 = 102 – 82
QR2 = `square - 64`
QR2 = `square`
QR = 6
यावरून, त्या भिंतीचा पाया व शिडीचे खालचे टोक यांमधील अंतर 6 मीटर आहे.
काटकोन त्रिकोणात काटकोन करणाऱ्या बाजू 9 सेमी व 12 सेमी आहेत, तर त्या त्रिकोणाच्या कर्णाची लांबी माहीत करण्यासाठी कृती पूर्ण करा.
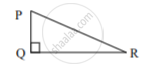
कृती: ∆PQR मध्ये, ∠PQR = 90°
पायथागोरसच्या प्रमेयानुसार,
PQ2 + `square` = PR2 .........…(i)
PR2 = 92 + 122
PR2 = `square + 144`
∴ PR2 = `square`
∴ PR = 15
त्रिकोणाचा कर्ण = `square`
समद्विभुज काटकोन त्रिकोणाच्या एकरूप बाजूंची लांबी 7 सेमी आहे. त्याची परिमिती काढा.
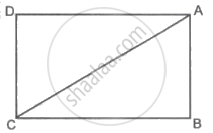
वरील आकृतीत `square`ABCD हा आयत आहे. जर AB = 5, AC = 13, तर बाजू BC ची लांबी काढण्यासाठी खालील कृती पर्ण करा.
कृती: ΔABC हा `square` त्रिकोण आहे.
∴ पायथागोरसच्या प्रमेयानुसार,
AB2 + BC2 = AC2
∴ 25 + BC2 = `square`
∴ BC2 = `square`
∴ BC = `square`
3 सेमी व 5 सेमी त्रिज्या आणि केंद्र O असलेली दोन एककेंद्री वर्तुळे काढा. मोठया वर्तुळावर कोणताही एक A बिंदू घ्या. बिंदू A मधून लहान वर्तुळाला स्पर्शिका काढा. त्या स्पर्शिकाखंडाची लांबी मोजा व लिहा. पायथागोरसच्या प्रमेयाचा उपयोग करून स्पर्शिकाखंडाची लांबी काढा.
