Advertisements
Advertisements
Question
समद्विभुज काटकोन त्रिकोणाच्या एकरूप बाजूंची लांबी 7 सेमी आहे. त्याची परिमिती काढा.
Solution
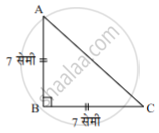
पक्ष: ∆ABC मध्ये, ∠ABC = 90°, AB = BC = 7 सेमी
शोधा: ∆ABC ची परिमिती
उकल:
∆ABC मध्ये, ∠ABC = 90° .....................[पक्ष]
∴ AC2 = AB2 + BC2 ..............[पायथागोरसचे प्रमेय]
∴ AC2 = (7)2 + (7)2
∴ AC2 = 49 + 49
∴ AC2 = 98
∴ AC = `sqrt(49 xx 2)` ............[दोन्ही बाजूंचे वर्गमूळ घेऊन]
∆ABC ची परिमिती = AB + BC + AC
= 7 + 7 + `7sqrt2`
= 14 + `7sqrt2` सेमी
∴ समद्विभुज काटकोन त्रिकोणाची परिमिती 14 + `7sqrt2` सेमी आहे.
APPEARS IN
RELATED QUESTIONS
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
काटकोन त्रिकोणात काटकोन करणाऱ्या बाजूंच्या वर्गांची बेरीज 169 असेल, तर त्याच्या कर्णाची लांबी किती?
बाजूंच्या लांबी a, b, c असलेल्या त्रिकोणामध्ये जर a2 + b2 = c2 असेल तर तो कोणत्या प्रकारचा त्रिकोण असेल?
काटकोन त्रिकोणामध्ये काटकोन करणाऱ्या बाजू 24 सेमी व 18 सेमी असतील तर त्याच्या कर्णाची लांबी ______ असेल.
आयताच्या बाजू 11 सेमी व 60 सेमी असतील, तर त्याच्या कर्णाची लांबी काढा.
प्रणाली आणि प्रसाद एकाच ठिकाणावरून पूर्व आणि उत्तर दिशेला सारख्या वेगाने निघाले. दोन तासांनंतर त्यांच्यामधील अंतर `15sqrt2` किमी असेल तर त्यांचा ताशी वेग काढा.
ΔABC मध्ये रेख AD ⊥ रेख BC आणि DB = 3CD, तर सिद्ध करा : 2AB2 = 2AC2 + BC2
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका समभुज चौकोनाच्या कर्णाची लांबी अनुक्रमे 60 व 80 असेल, तर त्या समभुज चौकोनाच्या बाजूची लांबी किती?
सोबतच्या आकृतीत, ∆ABC मध्ये, AD ⊥ BC, तर AB2 + CD2 = BD2 + AC2 हे सिद्ध करण्यासाठी खालील कृती पूर्ण करा.
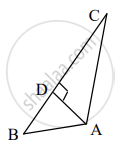
कृती: पायथागोरसच्या प्रमेयानुसार, काटकोन त्रिकोण ∆ADC मध्ये,
AC2 = AD2 + `square^2`
∴ AD2 = AC2 – CD2 …...........(i)
तसेच, पायथागोरसच्या प्रमेयानुसार, काटकोन त्रिकोण ∆ABD मध्ये,
AB2 = `square^2` + BD2
∴ AD2 = AB2 – BD2 …...… (ii)
∴ `square^2 - "BD"^2 = "AC"^2 - square^2` .....…….. (i) व (ii) वरून
∴ AB2 + CD2 = AC2 + BD2
3 सेमी व 5 सेमी त्रिज्या आणि केंद्र O असलेली दोन एककेंद्री वर्तुळे काढा. मोठया वर्तुळावर कोणताही एक A बिंदू घ्या. बिंदू A मधून लहान वर्तुळाला स्पर्शिका काढा. त्या स्पर्शिकाखंडाची लांबी मोजा व लिहा. पायथागोरसच्या प्रमेयाचा उपयोग करून स्पर्शिकाखंडाची लांबी काढा.
एका चौरसाचा कर्ण `10sqrt2` सेमी असतील तर त्याच्या बाजूची लांबी काढा.
