Advertisements
Advertisements
प्रश्न
समद्विभुज काटकोन त्रिकोणाच्या एकरूप बाजूंची लांबी 7 सेमी आहे. त्याची परिमिती काढा.
उत्तर
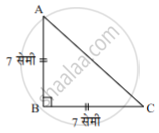
पक्ष: ∆ABC मध्ये, ∠ABC = 90°, AB = BC = 7 सेमी
शोधा: ∆ABC ची परिमिती
उकल:
∆ABC मध्ये, ∠ABC = 90° .....................[पक्ष]
∴ AC2 = AB2 + BC2 ..............[पायथागोरसचे प्रमेय]
∴ AC2 = (7)2 + (7)2
∴ AC2 = 49 + 49
∴ AC2 = 98
∴ AC = `sqrt(49 xx 2)` ............[दोन्ही बाजूंचे वर्गमूळ घेऊन]
∆ABC ची परिमिती = AB + BC + AC
= 7 + 7 + `7sqrt2`
= 14 + `7sqrt2` सेमी
∴ समद्विभुज काटकोन त्रिकोणाची परिमिती 14 + `7sqrt2` सेमी आहे.
APPEARS IN
संबंधित प्रश्न
आकृती मध्ये ∠DFE = 90°, रेख FG ⊥ रेख ED. जर GD = 8, FG = 12, तर (1) EG (2) FD आणि (3) EF काढा.
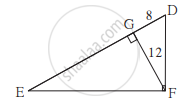
एका आयताची लांबी 35 सेमी व रुंदी 12 सेमी आहे तर त्या आयताच्या कर्णाची लांबी काढा.
समद्विभुज काटकोन त्रिकोणाची बाजू x आहे, तर त्याच्या कर्णाची लांबी काढा.
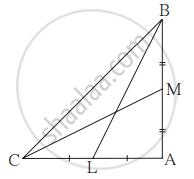
ΔABC मध्ये ∠BAC = 90°, रेख BL व रेख CM या ΔABC च्या मध्यगा आहेत, तर सिद्ध करा : 4(BL2 + CM2 ) = 5BC2.
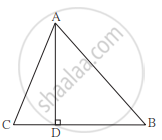
ΔABC मध्ये रेख AD ⊥ रेख BC आणि DB = 3CD, तर सिद्ध करा : 2AB2 = 2AC2 + BC2
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका चौरसाच्या कर्णाची लांबी `sqrt2` सेमी असेल, तर त्या चौरसाच्या प्रत्येक बाजूची लांबी किती?
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका आयताची एक बाजू 12 आणि कर्णाची लांबी 20 असेल, तर त्या आयताच्या दुसऱ्या बाजूची लांबी किती?
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका समभुज चौकोनाच्या कर्णाची लांबी अनुक्रमे 60 व 80 असेल, तर त्या समभुज चौकोनाच्या बाजूची लांबी किती?
एका आयताच्या बाजू अनुक्रमे 35 मीटर आणि 12 मीटर असल्यास त्याचा कर्ण किती?
सोबतच्या आकृतीत, ∆QPR मध्ये, ∠QPR = 90°, PM ⊥ QR, PM = 10, QM = 8 यावरून QR काढण्यासाठी खालील कृती पूर्ण करा.
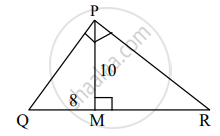
कृती:
∆PQR मध्ये, PM ⊥ QR
∠PMQ = 90°,
∆PMQ मध्ये, पायथागोरसच्या प्रमेयानुसार,
PM2 + `square` = PQ2 …(i)
∴ PQ2 = 102 + 82
∴ PQ2 = `square` + 64
PQ = `sqrt164`
∠PMR = 90°
यावरून, ∆QPR ~ ∆QMP ~ ∆PMR
∴ ∆QMP ~ ∆PMR
∴ `"PM"/"RM" = "QM"/"PM"`
∴ PM2 = RM × QM
∴ 102 = RM × 8
RM = `100/8 = square` आणि QR = QM + MR
QR = `square + 25/2 = 41/2`
