Advertisements
Advertisements
Question
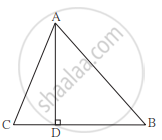
ΔABC मध्ये रेख AD ⊥ रेख BC आणि DB = 3CD, तर सिद्ध करा : 2AB2 = 2AC2 + BC2
Solution

पक्ष: रेख AD ⊥ रेख BC
DB = 3CD
साध्य: 2AB2 = 2AC2 + BC2
सिद्धता:
DB = 3CD ...(i) [पक्ष]
ΔADB मध्ये, ∠ADB = 90° ....[पक्ष]
∴ AB2 = AD2 + DB2 ....[पायथागोरसचे प्रमेय]
∴ AB2 = AD2 + (3CD)2 ........[(i) वरून]
∴ AB2 = AD2 + 9CD2 ...(ii)
AB2 – 9CD2 = AC2 – CD2
ΔADC मध्ये, ∠ADC = 90° ....[पक्ष]
∴ AC2 = AD2 + CD2 ...[पायथागोरसचे प्रमेय]
∴ AD2 = AC2 – CD2 ....(iii)
AB2 = AC2 – CD2 + 9CD2 ....[(ii) व (iii) वरून]
∴ AB2 = AC2 + 8CD2 ...(iv)
CD + DB = BC ....[C - D - B]
∴ CD + 3CD = BC .....[(i) वरून]
∴ 4CD = BC
∴ CD = `"BC"/4` ...(v)
AB2 = AC2 + 8`("BC"/4)^2` .....[(iv) व (v) वरून]
∴ AB2 = AC2 + `8 xx ("BC"^2)/16`
∴ AB2 = AC2 + `("BC"^2)/2`
∴ 2AB2 = 2AC2 + BC2 .....[दोन्ही बाजूंना 2 ने गुणून]
APPEARS IN
RELATED QUESTIONS
रस्त्याच्या दुतर्फा असलेल्या इमारतीच्या भिंती एकमेकींना समांतर आहेत. 5.8 मी लांबीच्या शिडीचे एक टोक रस्त्यावर ठेवले असता तिचे वरचे टोक पहिल्या इमारतीच्या 4 मीटर उंच असलेल्या खिडकीपर्यंत टेकते. त्याच ठिकाणी शिडी ठेवून रस्त्याच्या दुसऱ्या बाजूस वळविल्यास तिचे वरचे टोक दुसऱ्या इमारतीच्या 4.2 मीटर उंच असलेल्या खिडकीपर्यंत येते, तर रस्त्याची रुंदी काढा.
बाजूंच्या लांबी a, b, c असलेल्या त्रिकोणामध्ये जर a2 + b2 = c2 असेल तर तो कोणत्या प्रकारचा त्रिकोण असेल?
एका काटकोन त्रिकोणामध्ये काटकोन करणाऱ्या बाजू 9 सेमी व 12 सेमी आहेत, तर त्या त्रिकोणाच्या कर्णाची लांबी काढा.
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका चौरसाच्या कर्णाची लांबी `sqrt2` सेमी असेल, तर त्या चौरसाच्या प्रत्येक बाजूची लांबी किती?
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका समभुज चौकोनाच्या कर्णाची लांबी अनुक्रमे 60 व 80 असेल, तर त्या समभुज चौकोनाच्या बाजूची लांबी किती?
एका काटकोन त्रिकोणामध्ये काटकोन करणाऱ्या बाजू 24 सेमी व 18 सेमी असतील, तर त्याच्या कर्णाची लांबी काढा.
एका आयताचे क्षेत्रफळ 192 चौसेमी असून त्याची लांबी 16 सेमी आहे, तर त्या आयताच्या कर्णाची लांबी माहीत करण्यासाठी कृती पूर्ण करा.
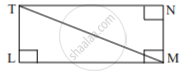
कृती: सोबतच्या आकृतीत, `square`LMNT हा आयत आहे.
आयताचे क्षेत्रफळ = लांबी × रुंदी
∴ आयताचे क्षेत्रफळ = `square` × रुंदी
रुंदी = 12 सेमी
∠TLM = 90° [आयताचा प्रत्येक कोन काटकोन असतो.]
∆TLM मध्ये, पायथागोरसच्या प्रमेयानुसार,
TL2 + `square` = TM2
TM2 = `square` + 122
TM2 = `square` + 144
TM = 20
∆LMN मध्ये, l = 5, m = 13, n = 12, तर ∆LMN हा काटकोन त्रिकोण आहे किंवा नाही ते ठरवण्यासाठी कृती करा. [l, m, n या ∠L, ∠M, व ∠N यांच्या समोरील बाजू आहेत.]
कृती: ∆LMN मध्ये, l = 5, m = 13, n = `square`
l2 = `square`, m2 = 169; n2 = 144.
l2 + n2 = 25 + 144 = `square`
`square^2` + l2 = m2
∴ पायथागोरसच्या प्रमेयानुसार, ∆LMN हा काटकोन त्रिकोण आहे.
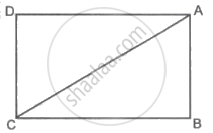
वरील आकृतीत `square`ABCD हा आयत आहे. जर AB = 5, AC = 13, तर बाजू BC ची लांबी काढण्यासाठी खालील कृती पर्ण करा.
कृती: ΔABC हा `square` त्रिकोण आहे.
∴ पायथागोरसच्या प्रमेयानुसार,
AB2 + BC2 = AC2
∴ 25 + BC2 = `square`
∴ BC2 = `square`
∴ BC = `square`
3 सेमी व 5 सेमी त्रिज्या आणि केंद्र O असलेली दोन एककेंद्री वर्तुळे काढा. मोठया वर्तुळावर कोणताही एक A बिंदू घ्या. बिंदू A मधून लहान वर्तुळाला स्पर्शिका काढा. त्या स्पर्शिकाखंडाची लांबी मोजा व लिहा. पायथागोरसच्या प्रमेयाचा उपयोग करून स्पर्शिकाखंडाची लांबी काढा.
