Advertisements
Advertisements
Question
एका समांतरभुज चौकोनाच्या लगतच्या दोन बाजूंच्या वर्गांची बेरीज 130 चौसेमी असून त्याच्या एका कर्णाची लांबी 14 सेमी आहे तर त्याच्या दुसऱ्या कर्णाची लांबी किती?
Solution
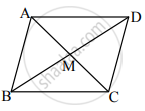
समजा, `square`ABCD हा समांतरभुज चौकोन आहे व त्यांचे कर्ण AC व BD एकमेकांना बिंदू M मध्ये छेदतात.
∴ AB2 + AD2 = 130 सेमी, BD = 14 सेमी
MD = `1/2` BD ...(i) [समांतरभुज चौकोनाचे कर्ण परस्परांना दुभागतात.]
= `1/2 xx 14 = 7` सेमी
ΔABD मध्ये, रेख AM ही मध्यगा आहे. ...[(i) वरून]
AB2 + AD2 = 2AM2 + 2MD2 ....[अपोलोनिअसचे प्रमेय]
∴ 130 = 2AM2 + 2(7)2
∴ 65 = AM2 + 49 ....[दोन्ही बाजूंना 2 ने भागून]
∴ AM2 = 65 – 49
∴ AM2 = 16
∴ AM = `sqrt(16)` ....[दोन्ही बाजूंचे वर्गमूळ घेऊन]
= 4 सेमी
आता, AC = 2 AM ....[समांतरभुज चौकोनाचे कर्ण परस्परांना दुभागतात.]
= 2 × 4 = 8 सेमी
∴ समांतरभुज चौकोनाच्या दुसऱ्या कर्णाची लांबी 8 सेमी आहे.
APPEARS IN
RELATED QUESTIONS
ΔPQR मध्ये, बिंदू S हा बाजू QR चा मध्यबिंदू आहे, जर PQ = 11, PR = 17, PS = 13 असेल तर QR ची लांबी काढा.
ΔABC मध्ये, AB = 10, AC = 7, BC = 9 तर बिंदू C मधून बाजू AB वर काढलेल्या मध्यगेची लांबी किती?
आकृती मध्ये, ΔABC च्या बाजू BC चा बिंदू M हा मध्यबिंदू आहे. जर AB2 + AC2 = 290 सेमी, AM = 8 सेमी, तर BC काढा.
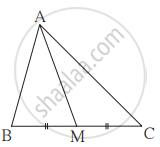
ΔABC मध्ये रेख AP ही मध्यगा आहे. जर BC = 18, AB2 + AC2 = 260 तर AP काढा.
आकृती मध्ये, M-Q-R-N. दिलेल्या माहितीवरून सिद्ध कराः PM = PN = `sqrt(3) xx "a"`

सिद्ध कराः समांतरभुज चौकोनाच्या कर्णांच्या वर्गांची बेरीज ही त्या चौकोनाच्या बाजूंच्या वर्गांच्या बेरजेबरोबर असते.
समद्विभुज त्रिकोणामध्ये एकरूप बाजूंची लांबी 13 सेमी असून त्याचा पाया 10 सेमी आहे, तर त्या त्रिकोणाच्या मध्यगासंपातापासून पायाच्या समोरील शिरोबिंदूपर्यंतचे अंतर काढा.
रेख PM ही ΔPQR ची मध्यगा आहे. जर PQ = 40, PR = 42 आणि PM = 29, तर QR काढा.
रेख AM ही ΔABC ची मध्यगा आहे. जर AB = 22, AC = 34, BC = 24, तर बाजू AM ची लांबी काढा.
ΔPQR मध्ये, रेख PM मध्यगा आहे. PM = 9 आणि PQ2 + PR2 = 290, तर QR काढा.
