Advertisements
Advertisements
Question
Block A of weight 2000N is kept on the inclined plane at 35° .It is connected to weight B by an inextensible string passing over smooth pulley.
Determine the weight of pan B so that B just moves down.Assume μ=0.2.
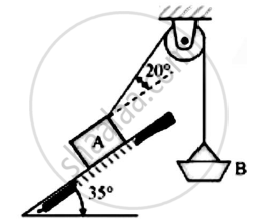
Given : Weight of block A=2000N
Angle of inclined plane = 35°
μ=0.2
To find : Weight of pan B
Solution
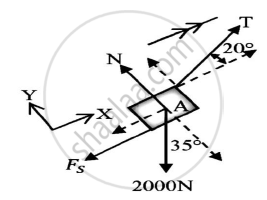
The pan B is in equilibrium
Applying the conditions of equilibrium
ΣFY=0
T-WB=0
T=WB ………..(1)
Applying the conditions of equilibrium on block A
ΣFY=0
N-WAcos35+Tsin20=0
From (1)
N=2000cos35-WBsin20 ………..(2)
FS=μsN
FS=0.2(2000cos35-WBsin20)
FS=400cos35-0.2WBsin20
Applying the conditions of equilibrium on block A
ΣFX=0
Tcos20-WAsin35-FS=0
WBcos20-2000sin35-(400cos35-0.2WBsin20)=0(From 1 and 2)
`W_B=(2000sin35+400cos35)/(cos20+0.2sin20)`
WB=1462.9685 N
The weight of pan B so that pan B just moves down is 1462.9685 N
APPEARS IN
RELATED QUESTIONS
Find the support reactions at A and B for the beam loaded as shown in the given figure.
State Lami’s theorem.
State the necessary condition for application of Lami’s theorem.
Three blocks A,B and C of masses 3 kg,2 kg and 7 kg respectively are connected as shown.Determine the acceleration of A,B and C.Also find the tension in the string.
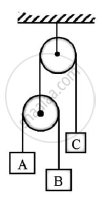
Given : mA=3kg
mB=2 kg
mC=7kg
To find: Acceleration of blocks A,B and C
A rod AD of length 40 cm is suspended from point D as shown in figure. If it has a weight of 25 N and also supports a load of 40N,find the tension in the cable using the method of virtual work.Take AC=30 cm.
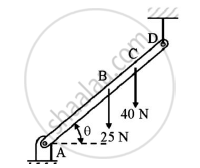
Given : Length of rod AD=40cm=0.4m
AC=0.3m
W=25N
Load on rod AD=40N
To find : Tension in the cable
