Advertisements
Advertisements
Question
Both the capacitors shown in figure are made of square plates of edge a. The separations between the plates of the capacitors are d1 and d2 as shown in the figure. A potential difference V is applied between the points a and b. An electron is projected between the plates of the upper capacitor along the central line. With what minimum speed should the electron be projected so that it does not collide with any plate? Consider only the electric forces.
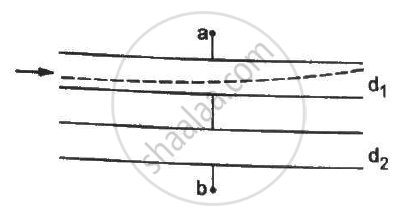
Solution
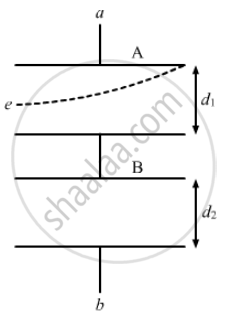
Let
Velocity of the electron = u
Mass of the electron = m
Now,
Horizontal distance, x = u × t
`⇒ t = x/v ..........(1)`
Let the electric field inside the capacitor be E
∴ Acceleration of the electron = `(qE)/m`
Vertical Distance, ` y = 1/2 (qE)/mt^2` = `1/2 (qE)/m(x/u)^2 ..........(∵ t = x/u)`
`y = d_1/2 and x = a`
`⇒ d_1/2 = 1/2 (qE)/m . (a/u)^2 .............(2)`
Capacitance of the two capacitors :-
`C_1 = (∈_0a^2)/(d_1) and C_2 = (∈_0a^2)/(d_2)`
It is given that the capacitors are connected in series.
Thus, the equivalent capacitance is given by
`C_(eq) = (C_1C_2)/(C_1+C_2)`
`C_(eq) = ((∈_0a^2)/d_1 xx (∈_0a^2)/d_2)/((∈_0a^2)/(d_1)+(∈_0a^2)/(d_2))` = `(∈_0a^2)/((d_1+d_2))`
Total charge on the system of capacitors, `Q = C_(eq)V =(∈_0a^2)/((d_1+d_2))V`
As the capacitors are in series, charge on both of them is the same.
The potential difference across the capacitor containing the electron is given by
`V = Q/C_1 = (∈_0a^2V)/(C_1(d_1+d_2) = (∈_0a^2V)/(((∈_0a^2)/d_1)(d_1+d_2)) = (Vd_1)/(d_1+d_2)`
The magnitude of the electric field inside the capacitor is given by `E = V/d_1 = V/(d_1+d_2)`
The charge on electron q is represented by e.
On putting the values of q and E in (2), we get
`⇒ d_1/2 = 1/2 (qV)/(m(d_1+d_2)) . (a/u)^2 ..........(3)`
The minimum velocity of the electron is given by
`u = ((Vea^2)/(md_1(d_1+d_2)))^(1/2)`
APPEARS IN
RELATED QUESTIONS
Define 1 volt PD.
Draw a labelled diagram of Van de Graaff generator. State its working principle to show how by introducing a small charged sphere into a larger sphere, a large amount of charge can be transferred to the outer sphere. State the use of this machine and also point out its limitations.
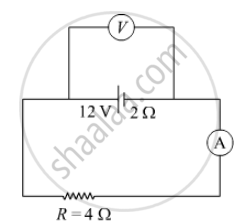
In the figure shown, an ammeter A and a resistor of 4 Ω are connected to the terminals of the source. The emf of the source is 12 V having an internal resistance of 2 Ω. Calculate the voltmeter and ammeter readings.
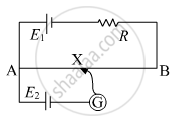
In the circuit diagram given below, AB is a uniform wire of resistance 15 Ω and length 1 m. It is connected to a cell E1 of emf 2V and negligible internal resistance and a resistance R. The balance point with another cell E2 of emf 75 mV is found at 30 cm from end A. Calculate the value of R.
Is there any restriction on the upper limit of the high voltage set up in Van de Graff generator machine? Explain.
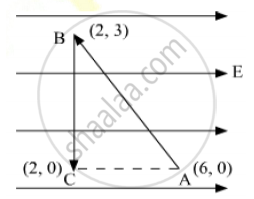
A test charge ‘q’ is moved without acceleration from A to C along the path from A to B and then from B to C in electric field E as shown in the figure. (i) Calculate the potential difference between A and C. (ii) At which point (of the two) is the electric potential more and why?
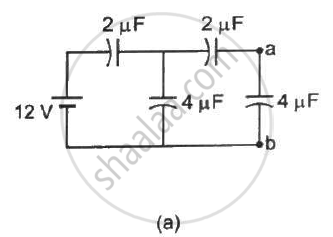
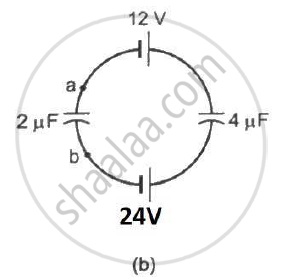
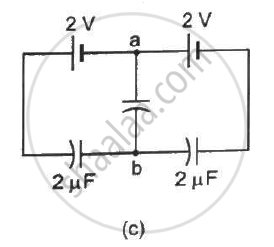
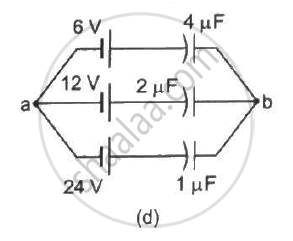
Find the potential difference `V_a - V_b` between the points a and b shown in each part of the figure.
Find the potential difference between the points A and B and between the points B and C of the figure in steady state.

A charge of `+2.0 xx 10^-8 C` is placed on the positive plate and a charge of `-1.0 xx 10^-8 C` on the negative plate of a parallel-plate capacitor of capacitance `1.2 xx 10^-3 "uF"` . Calculate the potential difference developed between the plates.
A charge of 1 µC is given to one plate of a parallel-plate capacitor of capacitance 0⋅1 µF and a charge of 2 µC is given to the other plate. Find the potential difference developed between the plates.
The capacitance between the adjacent plates shown in figure is 50 nF. A charge of 1⋅0 µC is placed on the middle plate. (a) What will be the charge on the outer surface of the upper plate? (b) Find the potential difference developed between the upper and the middle plates.

What will be the potential difference in the circuit when direct current is passed through the circuit?
If a positive charge moves in the direction of the electric field ______.
Two metal pieces having a potential difference of 800 V are 0.02 m apart horizontally. A particle of mass 1.96 × 10–15 kg is suspended in equilibrium between the plates. If e is the elementary charge, then charge on the particle is ______.
A and B are two points in an electric field. If the work done in carrying 4.0C of electric charge from A to B is 16.0 J, the potential difference between A and B is:
An α-particle and a proton are accelerate at same potential difference from rest. What will be the ratio of their final velocity?
On moving a charge of 20 C by 2 cm, 2 j of work is done then the potential difference between the point is:-
Work done in moving a unit positive charge through a distance of x meter on an equipotential surface is:-
