Question

Briefly explain the concept of the superposition principle.

Answer 1

When a jerk is given to a stretched string which is tied at one end, a wave pulse is produced and the pulse travels along the string. Suppose two persons holding the stretched string on either side give a jerk simultaneously, then these two wave pulses move towards each other, meet at some point and move away from each other with their original identity. Their behaviour is very different only at the crossing/meeting points; this behaviour depends on whether the two pulses have the same or different shape.
When the pulses have the same shape, at the crossing, the total displacement is the algebraic sum of their individual displacements and hence its net amplitude is higher than the amplitudes of the individual pulses. Whereas, if the two pulses have same amplitude but shapes are 180° out of phase at the crossing point, the net amplitude vanishes at that point and the pulses will recover their identities after crossing.

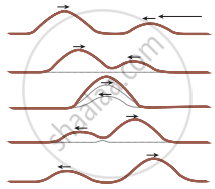
Superposition of two waves

Only waves can possess such a peculiar property and it is called superposition of waves. This means that the principle of superposition explains the net behaviour of the waves when they overlap. Generalizing to any number of waves i.e., if two are more waves in a medium move simultaneously, when they overlap, their total displacement is the vector sum of the individual displacements. We know that the waves satisfy the wave equation which is a linear second-order homogeneous partial differential equation in both space coordinates and time. Hence, their linear combination (often called as linear superposition of waves) will also satisfy the same differential equation. To understand mathematically, let us consider two functions which characterize the displacement of the waves, for example,

y₁ = A₁ sin (kx – ωt) and

y₂= A₂ cos (kx – ωt)

Since, both y₁ and y₂ satisfy the wave equation (solutions of wave equation) then their algebraic sum

y = y₁ + y₂

also satisfies the wave equation. This means, the displacements are additive. Suppose we multiply y₁ and y₂ with some constant then their amplitude is scaled by that constant Further, if C₁ and C₂ are used to multiply the displacements y₁ and y₂, respectively, then, their net displacement y is

C = C₁y₁ + C₂y₂

This can be generalized to any number of waves. In the case of n such waves in more than one dimension the displacements are written using vector notation. Here, the net displacement 

`vec"y" = sum_(i = 1)^"n" "C"_"i" vec"y"_"i"`

The principle of superposition can explain the following:

1. Space (or spatial) Interference (also known as Interference)
2. Time (or Temporal) Interference (also known as Beats)
3. Concept of stationary waves

Waves that obey principle of superposition are called linear waves (amplitude is much smaller than their wavelengths). In general, if the amplitude of the wave is not small then they are called non-linear waves. These violate the linear superposition principle, e.g., laser. In this chapter, we will focus our attention only on linear waves.