Advertisements
Advertisements
Question
Calculate the average velocity of the particle whose position vector changes from `vecr_1 = 5hati + 6hatj` to `vecr_2 = 2hati + 3hatj` in a time 5 second.
Solution
Given,
Position vectors of a particle
`vecr_1 = 5hati + 6hatj`,
`vecr_2 = 2hati + 3hatj`
time(t) = 5s
Solution:
Average velocity:
`vecV_"ave" = (Deltar)/(Deltat) = (vecr_2 - vecr_1)/(dt) = ((2 - 5)hati + (3 - 6)hatj)/5`
`vecV_"ave" = (-3hati - 3hatj)/5 = (-3)/5(hati + hatj)`
APPEARS IN
RELATED QUESTIONS
An object is dropped in an unknown planet from a height of 50 m, it reaches the ground in 2 s. The acceleration due to gravity in this unknown planet is ______
Define velocity.
Define acceleration.
What is the difference between velocity and average velocity?
Define angular velocity.
Derive the expression for centripetal acceleration.
The following table gives the range of a particle when thrown on different planets. All the particles are thrown at the same angle with the horizontal and with the same initial speed. Arrange the planets in ascending order according to their acceleration due to gravity, (g value).
| Planet | Range |
| Jupiter | 50 m |
| Earth | 75 m |
| Mars | 90 m |
| Mercury | 95m |
The following graphs represent the velocity-time graph. Identify what kind of motion a particle undergoes in each graph.
| (a) | 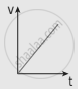 |
| (b) | 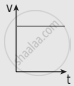 |
| (c) | 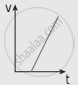 |
| (d) |  |
